(-1)×(-1)=+1 はなぜ成り立つか 〜その4〜
負の数の関係するかけ算についても、次の3つの法則が成り立つと「定義」する。
1.結合法則 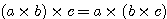
2.交換法則 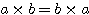
3.分配法則 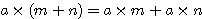 ただし + は、たし算を表す。
ただし + は、たし算を表す。
このとき、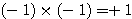 が成り立つことを「証明」してみよう。
が成り立つことを「証明」してみよう。
ただしその前にまず、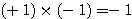 であることを証明しておく。
であることを証明しておく。
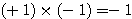 の証明
の証明
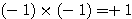 の証明
の証明
ということで、証明できた。
考えてみれば、実は高校数学でもこれと同じようにして「指数の拡張」をする。すなわち、
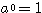 ・・・ (1),
・・・ (1), 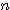 が正の整数であるとき
が正の整数であるとき 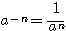 ・・・ (2)
・・・ (2)
という定義である。これは、指数が正の整数であるときに成り立つ次の「指数法則」を、0 以下の整数でも成り立つように定めた、ということである。
指数法則
1. 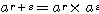 ,
, 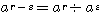
2. 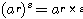
3. 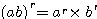
腕に覚えのある人は、「指数法則を用いて(1)(2)を証明する」ことに挑戦してみてはいかがだろうか。
Copyright (C) 2004- imasen, All rights reserved.