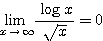 が成り立つことを証明するために、不等式を作ることである。すなわち、ある程度
が成り立つことを証明するために、不等式を作ることである。すなわち、ある程度 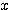 が大きいところで、
が大きいところで、極限の強弱の証明 〜その3〜 思案
目的は、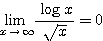 が成り立つことを証明するために、不等式を作ることである。すなわち、ある程度
が成り立つことを証明するために、不等式を作ることである。すなわち、ある程度 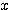 が大きいところで、
が大きいところで、
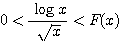 かつ
かつ 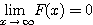
を満たす関数 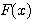 を見つけなくてはならない。
を見つけなくてはならない。
いろんな人を巻き込んで考えたがその作業は予想外に難航し、最終的に 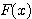 を見つけたのは筆者であった。筆者がどのように考えたか次に示してみるが、結構紆余曲折している。
を見つけたのは筆者であった。筆者がどのように考えたか次に示してみるが、結構紆余曲折している。
上のような 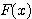 をいきなり見つけるのは難しいだろう。そこでまずは分母の
をいきなり見つけるのは難しいだろう。そこでまずは分母の 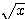 のことは考えず、
のことは考えず、
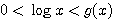 ・・・ (1)
・・・ (1)
を満たす関数 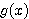 を見つけてみよう。ただし
を見つけてみよう。ただし 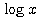 自身は単調増加で
自身は単調増加で 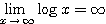 であるから、
であるから、
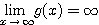
でなければならない。
しかも(1)式の辺々を 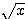 で割ることにより得られる不等式
で割ることにより得られる不等式
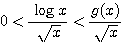
においてはさみうちにできるためには、
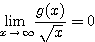
でなければならない。
さて、とりあえず 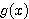 として最も簡単そうな関数は、
として最も簡単そうな関数は、
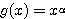 (
(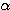 は実数)
は実数)
のような関数であろう。なぜならば、
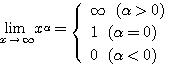
のように、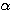 の値によって極限がいろいろと変わるからである。
の値によって極限がいろいろと変わるからである。
このように 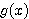 をおくとき、
をおくとき、
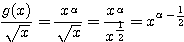
であるから、
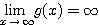 となるためには、
となるためには、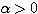
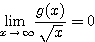 となるためには、
となるためには、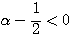 すなわち
すなわち 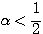
まとめて、 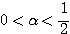
が成り立たなければならない。
ということはこれを満たす 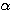 として、たとえば
として、たとえば 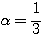 をとり、
をとり、
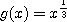
とすればよいのではないだろうかと考えてみた。
Copyright (C) 2004- imasen, All rights reserved.