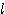 に下ろした垂線の足とし、O から
に下ろした垂線の足とし、O から 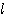 までの距離(垂線の長さ)を
までの距離(垂線の長さ)を 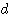 とする。このとき点 P が直線
とする。このとき点 P が直線 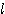 上のどこにあっても、つねに、∠OQQ0 =∠OP0P
上のどこにあっても、つねに、∠OQQ0 =∠OP0P
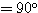 が成り立つ。
が成り立つ。反転の問題 〜その3〜
まず反転の性質(2)
O を通らない直線は、O を通る円に移る
を証明しよう。そこで(★)における点 P0 を、O から 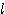 に下ろした垂線の足とし、O から
に下ろした垂線の足とし、O から 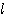 までの距離(垂線の長さ)を
までの距離(垂線の長さ)を 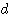 とする。このとき点 P が直線
とする。このとき点 P が直線 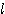 上のどこにあっても、つねに、∠OQQ0 =∠OP0P
上のどこにあっても、つねに、∠OQQ0 =∠OP0P
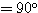 が成り立つ。
が成り立つ。
したがって円周角の定理の逆により、点 Q は線分 OQ0 を直径とする円周上に存在する。
さらに OP の長さが長くなるほど、OQ の長さは短くなるが、Q が O に一致することはない。したがって点 Q の軌跡は、線分 OQ0 を直径とする円周から、点 O を除いた図形である。
この証明をするに至った筆者の思考の流れは、
(1) 「軌跡が円である」ことを図形的に示すには、ほぼ円周角の定理の逆を利用することになるだろう。
そこである点
Q0 が存在して、∠OQQ0 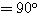 がいえるのではないだろうか。
がいえるのではないだろうか。
これが示せれば、円周角の定理の逆から、点
Q が線分 OQ0 を直径とする円周上を動くといえる。
(2) おそらく(★)が成り立ちそうな気がする(事実成り立つことが証明できた)。
そこで、
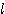 上の点 P,P0 に対して、∠OP0P
上の点 P,P0 に対して、∠OP0P
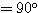 を満たす点 P0 を考えてみることにしよう。
を満たす点 P0 を考えてみることにしよう。
(3) P0 を、O から 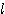 に下ろした垂線の足とすればよさそうだ。
に下ろした垂線の足とすればよさそうだ。
・・・というようなものである(実際はもう少し紆余曲折しているが^^;))。
さてそうすると反転の性質(3)もこれと逆の流れで証明できるはずだから、ここでは省略する。
したがって、次は反転の性質(4)を証明することにしよう。
Copyright (C) 2004- imasen, All rights reserved.