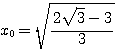 とおこう。問題は、
とおこう。問題は、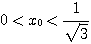 が成り立つかどうかである。
が成り立つかどうかである。イマセン第18回 忘れた頃にやってくる最大・最小 〜その5〜
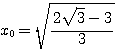 とおこう。問題は、
とおこう。問題は、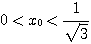 が成り立つかどうかである。
が成り立つかどうかである。
まず今までの過程から、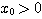 であることは明らかである。一方、
であることは明らかである。一方、
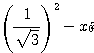
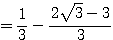
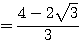
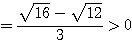
であるから、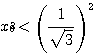 すなわち
すなわち 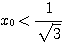 が成り立つ。
が成り立つ。
したがって、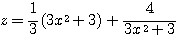 は、
は、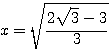 のとき最小値
のとき最小値 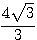 をとる。
をとる。
これを利用すると、
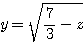
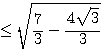
となるから、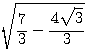 が最大値である。
が最大値である。
ところが実は、この二重根号は外すことができて、
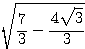
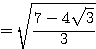
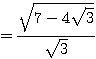
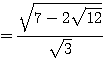 ← 中のルートの係数が 2 になるように変形。
← 中のルートの係数が 2 になるように変形。
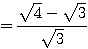 ←
← 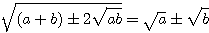 (複号同順。ただし
(複号同順。ただし 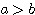 )
)
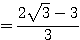 ← 有理化
← 有理化
したがって 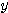 は、
は、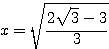 のとき最大値
のとき最大値 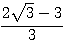 をとる。
をとる。
Copyright (C) 2004- imasen, All rights reserved.