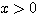 のとき
のとき 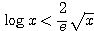 が成り立つことを示し、これを利用して
が成り立つことを示し、これを利用して 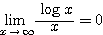 が成り立つことを示せ。
が成り立つことを示せ。極限の強弱の証明 〜その2〜 検索
強弱の関係自身を証明させる入試問題も、毎年多く出題される。たとえば次のようなものがある。
入試出題例1 京都工繊大(設問一部省略)
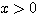 のとき
のとき 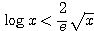 が成り立つことを示し、これを利用して
が成り立つことを示し、これを利用して 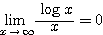 が成り立つことを示せ。
が成り立つことを示せ。
入試出題例2 武蔵工業大(設問一部省略)
(1) 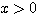 のとき
のとき 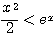 が成り立つことを証明せよ。
が成り立つことを証明せよ。
(2) 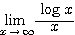 を求めよ。
を求めよ。
証明する方法は決まっていて、
[1] 不等式が成り立つことを、微分を用いて証明する。
[2] [1]で示した不等式を用いて、はさみうちの原理を利用する。
である。上記の例に[2]を実際に用いてみると次のようになる。([1]の証明はここでは省略する)
例1 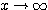 とするので、
とするので、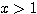 で考えてよい。このとき証明した不等式は
で考えてよい。このとき証明した不等式は 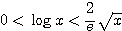 とできる。
とできる。
この不等式の辺々を 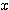 で割ると、
で割ると、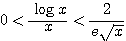 であり、
であり、
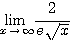
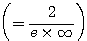
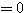 であるから、はさみうちの原理より
であるから、はさみうちの原理より 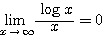 が成り立つ。
が成り立つ。
例2 まず 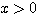 であることから、証明した不等式は
であることから、証明した不等式は 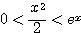 とできる。
とできる。
さらにこの不等式において 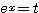 すなわち
すなわち 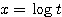 とおくと、
とおくと、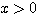 のとき
のとき 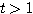 であるから、
であるから、
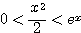
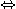
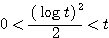
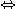
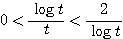 (両辺を
(両辺を 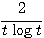 倍した)
倍した)
ここで 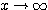 のとき
のとき 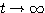 であり、
であり、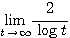
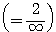
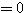 であるから、
であるから、
はさみうちの原理より 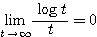 すなわち、
すなわち、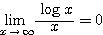 が成り立つ。
が成り立つ。
このように入試問題では、はさみうちにするための不等式があらかじめ与えられているので、安心してそれを用いて証明すればよい。
そして 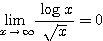 の証明方法も、流れ自体はこれと変わらないはずである。
の証明方法も、流れ自体はこれと変わらないはずである。
ところが今回は、その不等式すら与えられていないわけだから、まずそこから作り出すしかない。
これが意外と難しい作業だった。質問に来た本人だけでなく、その場にいた個別指導担当の大学生や、周りにいた生徒たちも巻き込んでいろいろ考え始めた(・・・巻き込まれた人たちにはさぞ迷惑な話であっただろう(^^;))。
Copyright (C) 2004- imasen, All rights reserved.