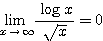極限の強弱の証明　〜その１〜　発端

　先日数学３まで学んでいる生徒の一人が、とある問題の中に 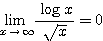と書かれているのを見つけ、これが成り立つ理由を知りたいと言ってやってきた。その問題では、それ自身の証明は要求されていなかったし、堂々と「成り立つことを用いてよい」とまで書いてあったが、個人的に証明してみたいということであった。

　数学３の入試問題を学んでいくと、これに限らず、次のような極限が必要となることが多い。

　　ア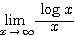：　　　　イ：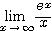　

　極限は基本的には「代入」すればよい。たとえば、

　　ウ：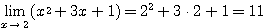　

　　エ：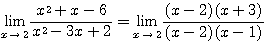　

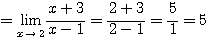
　　オ：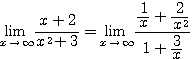　

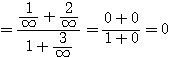
　などである。ただし、エやオはそのまま「代入」しても、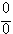 や 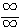 の形になって極限が決まらない。これを不定形というが、その場合でも上のようにうまく変形できれば、極限が求められることもある。

　ところがア・イは、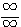 の形の不定形である上に、うまい変形もできない。もちろん生徒の持ってきた問題も同じである。

　このようなとき、もしも証明が要求されていなければ、次のような「強弱の関係」が知られていることを利用する。

＜極限における強弱の関係＞

　　　←　弱　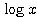　　≪　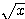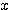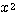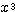・・・　≪　 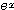,   ,   ,  　≪　・・・　≪　　　強　→

　すなわち、指数関数・対数関数・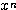 の影響力は、

　　●　指数関数が一番強く、対数関数が一番弱い。
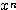　　●　 同士では、指数が大きいものほど強い。

※参考　指数関数・対数関数・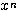 のグラフ。強いものほど、 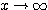のときに 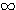への発散が速い（＝急カーブを描いている）。

　これを上の極限ア・イに用いるには、

　　ア：分母の 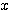の影響力のほうが強いので、分子 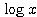を「定数」のようにみなし、

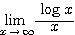
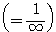
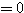
　　イ：分子 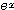の影響力のほうが強いので、分母 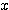を「定数」のようにみなし、

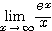
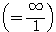
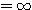
　というように考える。

　この「強弱の関係」に照らし合わせれば、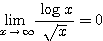 が成り立つことはすぐに分かる。ただし、それは証明にはならない。あくまでこの強弱はイメージに過ぎないからだ。

〜その２〜　検索　へ

Others TOPへ

Copyright (C) 2004- imasen, All rights reserved.