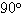がなくてはならない。そこで次のように考えた。反転の問題 〜その４〜
次に反転の性質(4)
O を通らない円は、O を通らない円に移る
を証明することにしよう。(2)の証明と同じように、三角形の相似を用いる。そしてどこかに
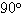がなくてはならない。そこで次のように考えた。
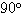を作るために、半直線 OP を、移す前の円の中心を通るように引こう。このとき図のように、直線と円との交点は2箇所できるから、O
から遠い所を P0、近い所を P1 とする。そしてそれに対応する
Q をそれぞれ Q0，Q1 とする。ただし
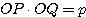(一定)より、Q0 の方が Q1 よりも
O に近い。
すると、移す前の円周上の P0，P1
以外の場所に点 P をとったとき、つねに ∠P0PP1
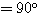となる。この点 P に対応する点を Q とする。
ここで(★)により、△OP0P∽△OQQ0，△OP1P∽△OQQ1 であるから次図で同じ印をつけた角は等しい。
△OP0P において、●＋○＋×＋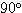
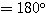であるから、●＋○＋× 
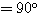である。したがって △OQQ1 において ∠Q0QQ1
= 
- (●＋○＋×) 
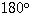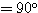が成り立つ。
したがって点 Q は、線分 Q0Q1 を直径とする円周上に存在する。
2点 Q0，Q1 自身も軌跡の一部であるから、点 Q の軌跡は上記の円全体であり、除外点はない。
Copyright (C) 2004- imasen, All rights reserved.