第1回 定積分と不等式 〜その4〜
問題2 ジョルダンの不等式の利用(大阪教育大)
(1) \( \displaystyle 0 \leq x \leq \frac{\pi}{2} \) に対して,\( \displaystyle e^{-x} \leq e^{-\sin x} \leq e^{-\frac{2x}{\pi}}\) を示せ.
(2) \( \displaystyle 1-\frac{1}{e} < \int_0^\frac{\pi}{2} e^{-\sin x} dx < \frac{\pi}{2} \left( 1-\frac{1}{e} \right) \) を示せ.
これも,考え方のみ示す.
<考え方>
この問題は(2)が本番であるが,それを示すための不等式を(1)で与えてあるので,楽である.(2)は,(1)で示した式の辺々を \( \displaystyle 0 \leq x \leq \frac{\pi}{2} \) で積分すれば終わりである.ただし,(1)の不等式は恒等的に成り立つわけではないので,積分した際に不等号から等号を取り除くことができる.さらに左側については,
\( \displaystyle \int_0^\frac{\pi}{2} e^{-x} dx = \left[ -e^{-x} \right]_0^\frac{\pi}{2} = 1 -\frac{1}{e^\frac{\pi}{2}} > 1 - \frac{1}{e} \)
のように,もう一段階ゆるく評価することになることにも注意しよう.
(1)を示すには,\( \displaystyle 0 \leq x \leq \frac{\pi}{2} \) において
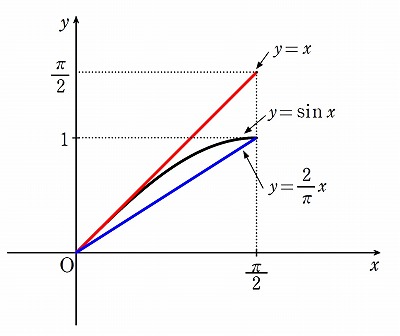
\( \displaystyle \frac{2}{\pi}x \leq \sin x \leq x \ \cdots \ (*) \)
が示せればよい.そうすれば辺々に \( -1 \) をかけて,「\( e \) の肩に乗せる」だけである.
不等式 \( (*) \) をジョルダンの不等式といい,これは下図のようにグラフを描いて示す.それだけでよい.

原題では(1)の前に
\( \displaystyle 0 \leq x \leq \frac{\pi}{2} \) に対して,\( \displaystyle \sin x \leq x \) を示せ.
という問いがあった.微分法を使えということであろうが,厳密にいうとジョルダンの不等式を認めた後に \( \left( \sin x \right)' = \cos x \) が導かれるため,微分法を用いると循環論法になってしまう.
Copyright (C) 2004- imasen, All rights reserved.