第1回 定積分と不等式 〜その5〜
問題3 接線と割線の利用(お茶の水女子大)
\(a,\ b\) を実数とし,\(a<b\) とする.関数 \(f(x)\) は閉区間 \([a,\ b]\) で連続,開区間 \((a,\ b)\) で少なくとも2回微分可能で,\(f''(x) \geq 0\) とする.
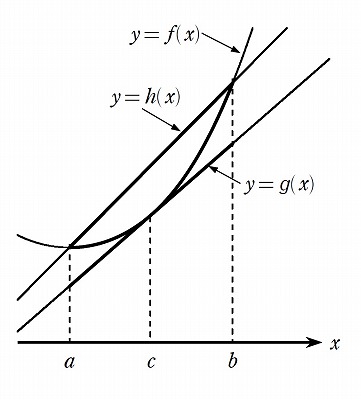
(1) \(a<c<b\) とする.\(y=g(x)\) を点 \((c,\ f(c))\) における \( y=f(x) \) の接線とする.\(a \leq x \leq b\) のとき,\(g(x) \leq f(x)\) を示せ.
(2) \(y=h(x)\) を,\((a,\ f(a))\),\((b,\ f(b))\) の2点を通る直線とする. \(a \leq x \leq b\) のとき,\(h(x) \geq f(x)\) を示せ.
(3) \(a<c<b\)
とする.
\( \displaystyle \frac{1}{2}(b-a)(f'(c)(a+b-2c)+2f(c)) \leq \int_a^b f(x)dx \leq \frac{1}{2}(f(a)+f(b))(b-a)\)
を示せ.
(4)\( \displaystyle \frac{\pi}{2} e^{-\frac{1}{\sqrt{2}}} \leq \int_0^\frac{\pi}{2} e^{-\cos x} dx \leq \frac{\pi}{4} \left(1+\frac{1}{e} \right) \)
を示せ.
<考え方>
(1)(2) \( y=f(x) \ \ (a \leq x \leq b) \) のグラフは「下に凸」であるから,
● 接線をどこで引いても,接線はグラフの上側にあることはない.
● 両端を通る直線は,グラフの下側にあることはない.

そのことは図形的にわかるが,ここでは式で示す流れを考えてみよう.ポイントは,
\( a \leq x \leq b \) において常に \( F(x) \geq 0 \) ⇔ \( a \leq x \leq b \) における \( F(x) \) の最小値が0以上
という言いかえをすることだ.
(1) 点 \((c,\ f(c))\) における \( y=f(x) \) の接線の方程式は
\( \displaystyle y=f'(c) (x-c) +f(c) \)
であるから,
\( \displaystyle g(x)=f'(c) (x-c) +f(c) \)
である.そこで,
\( \displaystyle G(x) = f(x)-g(x) = f(x) - \left\{ f'(c)(x-c) +f(c) \right\} \ \ \ (a \leq x \leq b) \)
とおくと,
\( \displaystyle G'(x) = f'(x) - f'(c) \)
である.
● \( \displaystyle G'(c) = 0 \) であること
● \( \displaystyle G''(x) = f''(x) \geq 0 \) により,\( G'(x) \) は(広義)単調増加であること
から,\( G'(x)=0 \) の解は \( x=c \) のただ1つであり,その前後で \( G'(x) \) の符号は負から正に変わる.
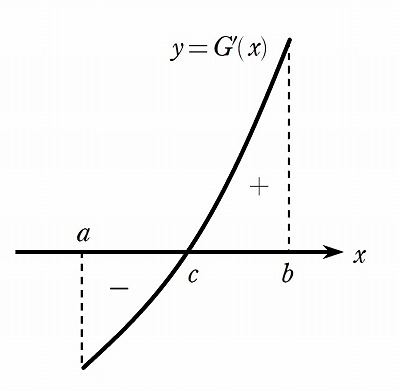
増減表を描いてみると,\( G(x) \) は \( x=c \) のときに最小となるとわかり,その最小値は,
\( \displaystyle G(c) = f(c) - \left\{ f'(c)(c-c) +f(c) \right\} =0 \)
である.したがって,\(a \leq x \leq b\) のとき,\(g(x) \leq f(x)\) であることが示された.(終)
(2) \((a,\ f(a))\),\((b,\ f(b))\) の2点を通る直線の方程式は,
\( \displaystyle y = \frac{f(b)-f(a)}{b-a}(x-a)+f(a) \)
であり,この右辺を整理することにより,
\( \displaystyle h(x) = \frac{f(b)-f(a)}{b-a}x + \frac{bf(a)-af(b)}{b-a} \)
である.そこで,
\( \displaystyle H(x) = h(x) -f(x) = \frac{f(b)-f(a)}{b-a}x + \frac{bf(a)-af(b)}{b-a} -f(x) \)
とおくと,
\( \displaystyle H'(x) = \frac{f(b)-f(a)}{b-a} -f'(x) \)
である.平均値の定理より,
\( \displaystyle f'(d) = \frac{f(b)-f(a)}{b-a} \) …(a) かつ \( \displaystyle a<d<b \) …(b)
を満たす \( d \) が少なくとも1つ存在する.
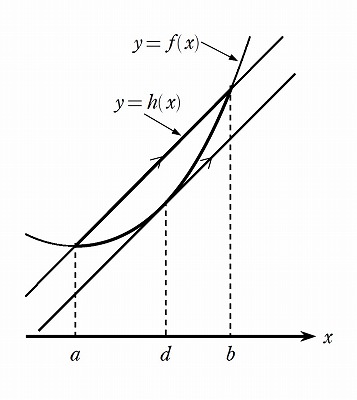
● この \( d \) に対して,\( \displaystyle H'(d) = 0 \) であること
● \( \displaystyle H''(x) = -f''(x) \leq 0 \) により,\( H'(x) \) は(広義)単調減少であること
から,\( H'(x)=0 \) の解は \( x=d \) のただ1つであり,その前後で \( H'(d) \) の符号は正から負に変わる.
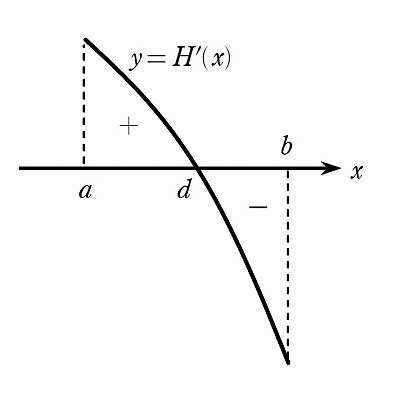
増減表を描いてみると,\( H(x) \) が最小になるのは \( x=a,\ b \) のいずれかのときとわかり,
\( \displaystyle H(a) = \frac{f(b)-f(a)}{b-a}a + \frac{bf(a)-af(b)}{b-a} -f(a) =0 \)
\( \displaystyle H(b) = \frac{f(b)-f(a)}{b-a}b + \frac{bf(a)-af(b)}{b-a} -f(b) =0 \)
により,最小値は0である.したがって,\(a \leq x \leq b\) のとき,\(h(x) \geq f(x)\) であることが示された.(終)
ちなみに,曲線と2点以上で交わる直線を,その曲線の「割線(かっせん)」というらしい.
この問題の(2)での直線 \( y = h(x) \) は,曲線 \( y = f(x) \) の割線ということになる.
長くなってしまったので,続きは次のページで.
Copyright (C) 2004- imasen, All rights reserved.