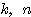 は
は 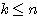 を満たす整数とするとき、
を満たす整数とするとき、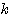 から
から 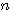 までの整数の個数 ・・・
までの整数の個数 ・・・ 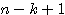 個
個イマセン第14回 数を数える〜2〜
問題1.解答
(1) 5から10まで整数の個数 ・・・ 6個
(2) 100から200までの整数の個数 ・・・ 101個
(3) 78から123までの整数の個数 ・・・ 46個
(4) 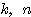 は
は 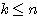 を満たす整数とするとき、
を満たす整数とするとき、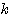 から
から 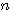 までの整数の個数 ・・・
までの整数の個数 ・・・ 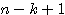 個
個
解説
よくある間違いでは、(1)5個 (2)100個 (3)45個 (4)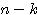 個 などのように、個数を単純に(最大の数)-(最小の数)としてしまうことだろうか。皆さんは大丈夫だったかな?
個 などのように、個数を単純に(最大の数)-(最小の数)としてしまうことだろうか。皆さんは大丈夫だったかな?
たとえば(1)で、実際指を折って数えてみてほしい。
5, 6, 7, 8, 9, 10
・・・実際は6個だろう?実は、このように数を数える問題は、簡単なようでいて自分もよく迷う。そして少しずれてしまうと、その後の問題に大きく影響してしまうのだ。
どうも人間というのは数を数えるのが苦手なようで、生徒もよくこの手の質問をしてくる。(1)のように比較的小さい個数だったらいいけれど、(2)(3)のように個数が大きくなったり、(4)のように文字になったりしたら、実際に指で数えるわけにはいかないのでお手上げである。
そこで、公式めいたものを一つ。
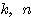 は
は 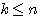 を満たす整数とするとき、
を満たす整数とするとき、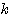 から
から 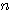 までの整数の個数は、
までの整数の個数は、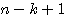 である。すなわち、
である。すなわち、
「最小の数」を個数に含めるとき (個数)=(最大の数)-(最小の数)+1 ・・・(*)
たとえば問題1では、
(1) 10-5+1=6 (2) 200-100+1=101 (3) 123-78+1=46
もっともこれは、小さい個数で実験して得られた経験則に過ぎない。でも結構役に立つ。次以降では、この(*)を問題2や3にも応用してみよう。
Copyright (C) 2004- imasen, All rights reserved.