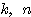 は
は 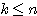 を満たす整数とするとき、
を満たす整数とするとき、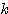 から
から 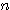 までの整数の個数
までの整数の個数イマセン第14回 数を数える〜1〜
「1から100までの整数の個数」は、100個である。それならばすぐ分かるが、整数を途中から数え始めると意外ときちんと数えられないことに気づくはず。次の問題で試してほしい。
問題1.次の個数を求めよ。
(1) 5から10まで整数の個数
(2) 100から200までの整数の個数
(3) 78から123までの整数の個数
(4) 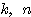 は
は 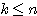 を満たす整数とするとき、
を満たす整数とするとき、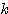 から
から 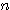 までの整数の個数
までの整数の個数
問題2.次の整数を求めよ。(数学的にはやや不正確な表現かもしれないが、一般的な解釈で考えてほしい)
(1) 100を1番目として、5番目の整数
(2) 100から5個先の整数
(3) 96を1番目として、23番目の整数
(4) 96から23個先の整数
問題3.順列 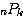 (異なる
(異なる 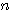 個のものから
個のものから 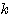 個を選んで一列に並べる並べ方の総数)の計算法則は次の通りである。
個を選んで一列に並べる並べ方の総数)の計算法則は次の通りである。
(例)
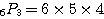 Pの左の数字6から始め、一つずつ数を減らしながら、右の数字3個分掛ける。
Pの左の数字6から始め、一つずつ数を減らしながら、右の数字3個分掛ける。
すなわち他の例で言えば、
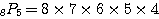 ,
, 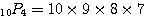 ,
,
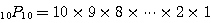 ということである。
ということである。
最後 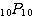 は途中を・・・と書いて省略した。式が長くなる場合、そのように書くことも多い。
は途中を・・・と書いて省略した。式が長くなる場合、そのように書くことも多い。
このとき、次の式のAからEに入る数・式は何か。
(1) 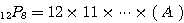
(2) 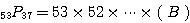
(3) 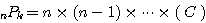
(4) 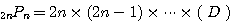
(5) 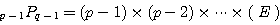 (ただし
(ただし 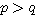 とする)
とする)
できれば、指を一つひとつ折って数えたり、すべてを紙に書き出したり、という解き方はぜひしないでほしい。もちろんしてもいいけれど、そこから何か法則が得られないだろうか?と考えてみてほしい。
Copyright (C) 2004- imasen, All rights reserved.