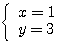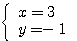
イマセン第１０回　連立方程式<2>〜その３〜

解答

(2) 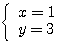　または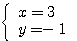　

解説

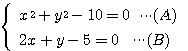
２次以上の文字がある連立方程式を解くには、基本的に消去法を用いるしかない。その基本を忘れて、両方の式が =0 で等しいからという理由だけで、

    ×××　

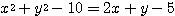
とつなげた式を書いていた人を見たことがある。これでは 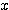も 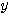もどちらも消えずに残ってしまう。無目的に式をいじるのだけはやめよう。

基本に忠実に。(B)の式は１次なので、こちらを変形して

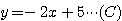
とし、これを(A)に代入しよう。

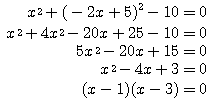
    したがって、　・・・(*)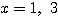

    (i)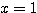のとき

    (B)に代入して、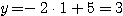

    (ii)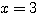のとき

    (B)に代入して、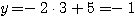

    よって、　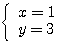　または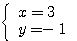　

さて、(*)まで出た段階で、(B)式に代入して答えを導いた。確かに(B)式のほうが簡単な式だから、何となくこちらに代入して正解していた人も多いだろう。だが、それを(A)式に代入してはいけないのだろうか？

答えは「ダメ！」

なぜか。実際代入してみよう。

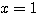     を(A)に代入して、

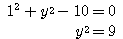
    したがって、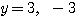

理由が分かっただろうか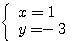？は(B)を満たさないので、これは解とはいえない。本来 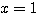のとき 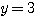のみが答えであったのに、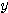（ の）２次式である(A)を使ってしまうことにより、 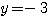という余計な答えが出てしまうのだ。片方の文字の答えが出たら、それは必ず「最も次数の低い式」に代入するのが鉄則。単に計算が楽なだけで(B)を選んだわけではないのだ。

その２（解答編）へ

その４（補足編）へ

イマセンTOPへ