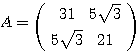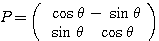，
に対して、
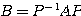とする。直交行列による対称行列の対角化（補足編）
以上のようなことを書いていたら、実は06年度大学入試問題に、この内容をそのまま題材にした問題が出題された。この年度から課程が新しくなり、「１次変換」が出題範囲となったからであろう。
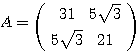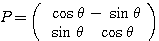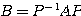問題 2つの行列 ， に対して、 とする。
(1) 
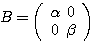となるように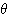 
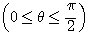の値を定め、
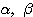の値を求めよ。
(2) (1)で求めた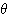 
を用いて、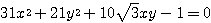
の表す曲線を、原点の周りに 
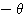だけ回転移動して得られる曲線の方程式を求めよ。
(06 旭川医大)
解答
(1) 
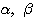は対称行列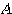 
の固有値である。固有方程式 
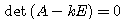を解き、
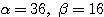とする。
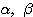に対する固有ベクトルで、絶対値が1のものをそれぞれ、
，
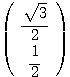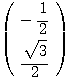とする。
このとき、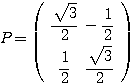
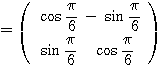とできるので、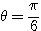 
(2) 与えられた行列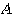 
に対し、
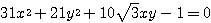
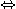
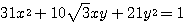
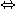
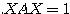
とでき、これを原点周りに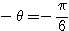 
回転させると、標準形になることが分かる。このときの求める標準形は、
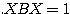
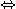
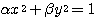
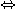
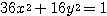
となる。
Copyright (C) 2004- imasen, All rights reserved.