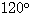トレミーの定理の証明～１～

例題　四角形ABCDは円に内接していて、AB=3, BC=7, CD=7, DA=5 とする。次の値を求めよ。
（ア） ∠Aの大きさ　　（イ） BDの長さ　　（ウ） ACの長さ
（センター試験・追試　の一部）

解答は（ア）∠A=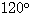　（イ）BD=7　　△ABDと△BCDで余弦定理を2式立てて、連立すればよい。

円に内接する四角形001

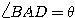, BD=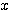 とおく。△ABDと△BCDで余弦定理を用いて、
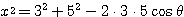　　・・・(1)
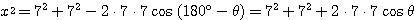　　・・・(2)
(1)(2)より、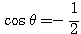　すなわち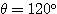が得られ、これを(1)または(2)に代入して、　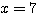を得る。

（ウ）では、「正統派」の解法をするならば、改めて△ABCと△ACDで余弦定理を立てて連立する。

円に内接する四角形002

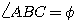, AC=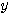 とおく。△ABCと△ACDで余弦定理を用いて、
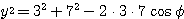　　・・・(3)
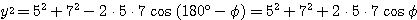　　・・・(4)
(3)(4)より、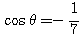　が得られ、これを(3)または(4)に代入して、　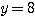を得る。

　ところがそれでは計算の手間が2倍に増え、一刻を争うセンター試験などでは特に、痛々しい事態となる。

　そこで（ウ）では、教科書に表立っては載っていない次のような定理を使うと早い。

＜トレミーの定理＞
円に内接する四角形ABCDにおいて、
　AB･CD+AD･BC=AC･BD
が成立する。

トレミーの定理の図

これを利用すると、3･7+5･7=AC･7 より、AC=8 とすぐに求めることができる。

　特にセンター試験では、「円に内接する四角形」はよくある構図で、この「トレミーの定理」を知っていると問題がスムーズに解けることが多い。だが、自分はその証明を知らず、数学教師としてそれはマズイので、何とか自力で証明を試みたのだった。