イマセン第21回 動くものがたくさんあるときは 〜その3〜
次に、計算で行く解法を紹介しよう。ベクトルを用いるのが一番だろう。
解答1.(解2・計算で行く解法)
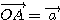 ,
,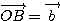 ,
,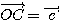 とおく。このとき
とおく。このとき
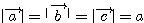 ,
,
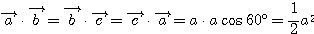
である。
点 P が辺 AB 上、点 Q が 辺 OC 上をそれぞれ動くことから、
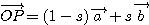 ただし
ただし 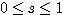
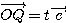 ただし
ただし 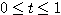
と表せる。よって、
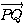 =
= 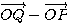
= 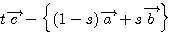
= 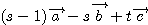
と表せる。このとき、
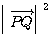 =
= 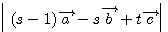
=
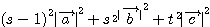
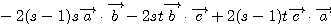
=
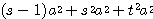
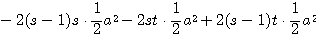
=
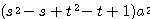
となる。
ここで 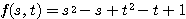 とおくと、
とおくと、
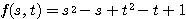
=
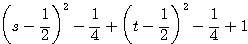
=
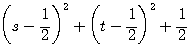
であり、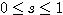 ,
,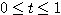 であることから
であることから 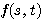 の最小値は
の最小値は
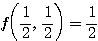
である。
したがって、PQ=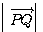 の最小値は
の最小値は
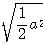 =
= 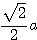
となる。
見た目こそややこしくなったが、これは単なる「2変数関数の最大最小」の問題である。
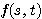 の最小値を考えるときに少々荒っぽくやってしまったが、もう少し丁寧にやると次のようになる。
の最小値を考えるときに少々荒っぽくやってしまったが、もう少し丁寧にやると次のようになる。
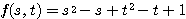
=
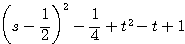 ・・・ まずは
・・・ まずは 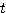 を固定し、
を固定し、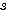 だけの関数と考えて平方完成
だけの関数と考えて平方完成
= 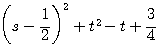 ・・・ この式から
・・・ この式から 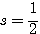 のとき最小値
のとき最小値 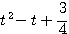 をとるとわかる。
をとるとわかる。
=
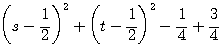 ・・・ 次に、
・・・ 次に、 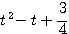 を
を 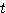 の関数と考えて平方完成
の関数と考えて平方完成
=
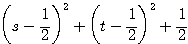 ・・・ この式から
・・・ この式から 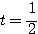 のとき最小値
のとき最小値 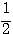 をとるとわかる。
をとるとわかる。
つまり、
「まずは 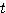 を固定し、
を固定し、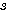 だけ動かす」 → 「次に
だけ動かす」 → 「次に 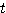 を動かす」
を動かす」
という点で、結局ここでも「動くものを1つだけにする」という考え方が登場している。
また、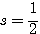 ,
,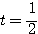 で最小になるということは、それぞれ、「点 P が辺 AB の中点」「点 Q が辺 OC
の中点」にあるときが最小である、ということを表していて、これは解1で図形的に考えたときと同じ結果である。
で最小になるということは、それぞれ、「点 P が辺 AB の中点」「点 Q が辺 OC
の中点」にあるときが最小である、ということを表していて、これは解1で図形的に考えたときと同じ結果である。
Copyright (C) 2004- imasen, All rights reserved.