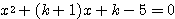・・・(*)イマセン第16回 条件をそろえよう〜４〜
ところでこの問題を、次のように解いてみたらどうだろう？
********************************************************************
（解答） 方程式
・・・(*)
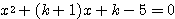において、解の1つを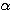
とする。その平方
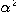も解であるから、
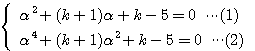
ここから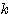
を消去するために、(1)を
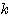について整理して、
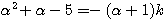
ここで、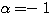
はこの方程式を満たさない（右辺は0だが左辺は0以外になる）ので、両辺を
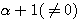で割ると、
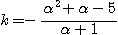・・・(3)
これを(2)に代入して、
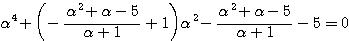
分母を払って整理する（途中経過はかなり省略する）と、
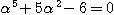
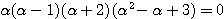
よって、この方程式の実数解は、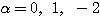
・・・(**)
これらをそれぞれ(3)に代入して、
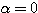のとき 
、
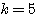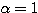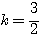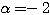のとき 
、
のとき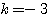 
。
********************************************************************
さて、ここで解答を終了させて「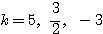
」を答えにしてしまうと、〜２〜で求めた正答（
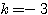のみ）と照らし合わせても分かるとおり、誤答である。
一見文字の個数=式の個数であるからきちんと解けたように見える。どういうことだろうか。
本当の答えは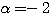
だけなのだが、
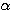の値が3つも出てきてしまった。実はこの解答には続きがある。
********************************************************************
（解答続き）
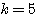のとき方程式(*)は 
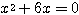となり、この2解は 
。
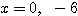よって条件を満たさず不適。
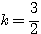のとき方程式(*)は 
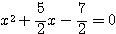となり、この2解は 
。
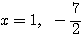よって条件を満たさず不適。
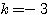のとき方程式(*)は 
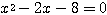となり、この2解は 
。
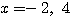これは条件を満たすので適する。
以上より、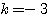
********************************************************************
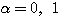のとき、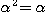
である。このとき(1)(2)は（見た目こそ違うが）まったく同じ式である。
つまり「少なくとも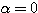
(または1)を解に持つときの
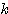の値」を求めているに過ぎず、このとき他方の解についてはまったく考えられていない。
したがって(1)(2)だけでは「一方の解が他の解の平方」という条件をきちんと満たしているとは言えない（場合によって式の個数が減ってしまう）。だから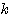
の値を求めた後、改めてこの条件を満たすかを、方程式(*)に戻って確認しないといけないのだ。
とりあえず求められた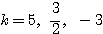
を改めて(*)に代入して、「
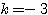であれば確かに条件を満たす」ということが導かれた。これを「十分性の確認」という。
Copyright (C) 2004- imasen, All rights reserved.