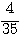 と
と 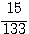 の大小を比較せよ。(小学校)
の大小を比較せよ。(小学校)解答2.
他の単元での問題をやっているときにも必ず登場するような計算であり、しかも短時間で正確にできる人はあまり多くないと思う。
学校の定期テストを受けた生徒がよく言うセリフ、「時間が足りなかった」。
と言う事は、計算練習をしていればすぐ解けるようになるという問題である。
(1) 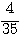 と
と 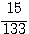 の大小を比較せよ。(小学校)
の大小を比較せよ。(小学校)
→まず通分する。それを思いつかない人も結構多い。
ただし 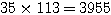 と単純に分母を掛け算するのは考えもの。
と単純に分母を掛け算するのは考えもの。
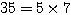 ,
, 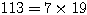 と素因数分解できることを考え、
と素因数分解できることを考え、
最小公倍数 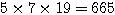 を分母にする。
を分母にする。
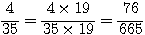
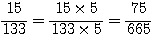
より、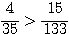 である。
である。
(2) 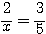 のとき、
のとき、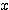 を求めよ。(中学校)
を求めよ。(中学校)
両辺の逆数同士も等しい。最近は中学校で習わないのかな?
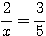 より、
より、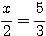
両辺に2を掛けて、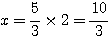 である。
である。
(3) 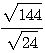 の分母を有理化せよ。(中学校)
の分母を有理化せよ。(中学校)
分母分子に 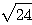 を掛けたりはしないだろう。まずルートの中身を極力小さくする。
を掛けたりはしないだろう。まずルートの中身を極力小さくする。
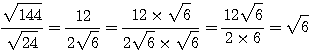
さらに多少裏技的に、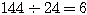 を利用して、いきなり
を利用して、いきなり
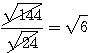
としてしまう手もある。
(4) 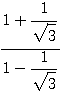 の分母を有理化せよ。(高校)
の分母を有理化せよ。(高校)
これは、分数の中に分数があり、さらにルートが出てくるので、一筋縄ではいかない。
この解答は、今はナイショ。