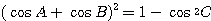
三角形の形状決定 〜その4〜
補足編:
以上のことを、某校舎で一緒になるF先生にお話しした。F先生と私は、それぞれ違う校舎で同じテキストを担当していて、以前「この問題、三角比の方法で解けないですかね」と話していたのだ。今回のテーマは、その話の中から生まれたと言える。
「全部 cos に直すとできました。でも、全部展開したら壮絶な式になっちゃって・・・、もっとスマートにできるといいんですけど」
と言ったら、F先生が示してくれた解答は次の通りだ。まず、両辺それぞれを因数分解するところから始める。もちろんそれでも計算量は多いが、それでも私の方法よりはずっと楽だ。さすがだ。
解答:
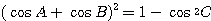
に余弦定理を代入した
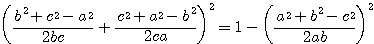 ・・・(***)
・・・(***)
において、
左辺の( )の中 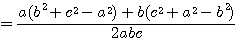
となる。この式の分子は因数分解できて、
分子 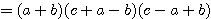
となる。したがって、
左辺 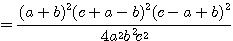 ・・・(1)
・・・(1)
となる。一方右辺について、
右辺 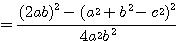
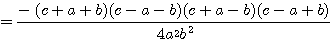 ・・・(2)
・・・(2)
となる。(1)(2)を(***)に代入して、
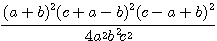
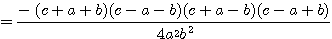
分母を払い、さらに両辺を 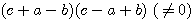 で割ると、
で割ると、
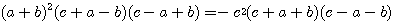
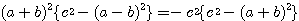
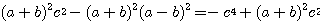
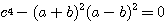
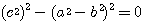
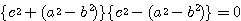
したがって、
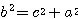 または
または 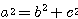
となる。
Copyright (C) 2004- imasen, All rights reserved.