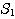 と,点 A を中心とする半径 1 の円を
と,点 A を中心とする半径 1 の円を 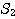 がある.
がある.カージオイドとサイクロイド 〜その1〜
テキストを作るのにいろいろな問題を見ていたら,次の問題に出会った.
xy 平面上に原点 O を中心とする半径 1 の円 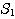 と,点 A を中心とする半径 1 の円を
と,点 A を中心とする半径 1 の円を 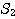 がある.
がある.
円 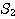 は円
は円 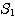 に外接しながら,滑ることなく円
に外接しながら,滑ることなく円 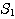 のまわりを反時計回りに一周する.
のまわりを反時計回りに一周する.
点 A の出発点は (2, 0) であり,円 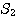 上の点で,このとき (1, 0) に位置している点を P とする.
上の点で,このとき (1, 0) に位置している点を P とする.
点 A が (2, 0) から出発し,(2, 0) に戻ってくるとき,点 P のえがく曲線を
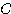 とすると,図のようになる.
とすると,図のようになる.
また,動径 OA と x 軸の正の部分とのなす角が 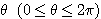 であるときの点 P の座標を
であるときの点 P の座標を 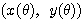 とする.
とする.
このとき,次の問いに答えよ.
(1) 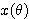 ,
,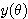 を
を 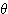 を用いて表せ.
を用いて表せ.
(09 長崎大・(2)以降は省略)
まずは,この問題に答えてみよう.以前に「ベクトルをつなぐ」で紹介したとおりの方法を用いる.
コツは下図のように,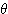 を小さめにとった図をかいてみることである.
を小さめにとった図をかいてみることである.
図において,弧PP'' と弧 P'P'' の長さが等しいことから,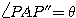 となることが分かるだろう.
となることが分かるだろう.
あとは図の中に書いてる説明をよく読んでほしい.
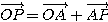
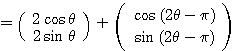
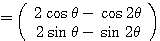
となるから,
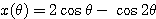 ,
, 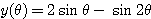 ・・・(答)
・・・(答)
である.
そしてこの曲線 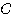 を,サイクロイドという.
を,サイクロイドという.
Copyright (C) 2004- imasen, All rights reserved.