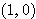 にあり、反時計回りにほどける。いま糸をたわむことなくほどいていき、その糸と円の接点を
Q とし、
にあり、反時計回りにほどける。いま糸をたわむことなくほどいていき、その糸と円の接点を
Q とし、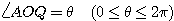 とする。さらに、ほどかれた糸の端の座標を P
とする。さらに、ほどかれた糸の端の座標を P 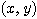 とする。このとき、
とする。このとき、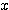 と
と 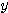 を
を 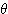 の関数で表せ。
の関数で表せ。イマセン第22回 ベクトルをつなぐ 〜その1〜
今回は数学3Cを利用する理系難関校志望者を対象にしたいと思う。
曲線の式や図がすでに与えられていれば、面積や体積を積分を用いて求めることはできるが、その式を自分で作らなくてはならない場合、それとは別の大きな難しさが存在する。今回はそんな問題を扱ってみよう。
問題
1.原点 O を中心とする半径 1 の円に糸が巻きつけられていて、糸の端は点 A
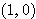 にあり、反時計回りにほどける。いま糸をたわむことなくほどいていき、その糸と円の接点を
Q とし、
にあり、反時計回りにほどける。いま糸をたわむことなくほどいていき、その糸と円の接点を
Q とし、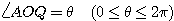 とする。さらに、ほどかれた糸の端の座標を P
とする。さらに、ほどかれた糸の端の座標を P 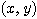 とする。このとき、
とする。このとき、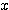 と
と 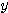 を
を 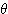 の関数で表せ。
の関数で表せ。
2. 原点 O を中心とする半径 1 の円周上に動点 Q がある。Q は第1象限にある円周上を点A
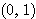 から点B
から点B 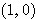 まで動くとし、
まで動くとし、 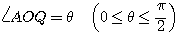 とする。さらに、点 Q を中心として線分 OQ と時計回りに角
とする。さらに、点 Q を中心として線分 OQ と時計回りに角 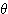 をなす長さ 1 の線分 QP を考え、P
をなす長さ 1 の線分 QP を考え、P 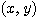 とする。このとき、
とする。このとき、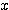 と
と 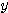 を
を 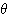 の関数で表せ。
の関数で表せ。
Hint: 次のFactが成り立つことを利用しよう。
<Fact>点 O を原点とする座標平面上の点 P 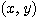 に対し、線分 OP の長さを
に対し、線分 OP の長さを 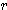 ,線分 OP が
,線分 OP が 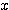 軸正の向きとなす角を
軸正の向きとなす角を 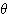 とするとき、
とするとき、
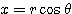 ,
, 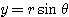 すなわち、
すなわち、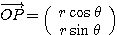
が成り立つ。このとき、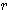 を
を 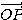 の絶対値、
の絶対値、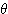 を
を 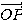 の偏角という。
の偏角という。
ただし偏角は、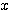 軸正の向きから反時計回りに測るとき正、時計回りに測るとき負である。
軸正の向きから反時計回りに測るとき正、時計回りに測るとき負である。
Copyright (C) 2004- imasen, All rights reserved.