通り番外編 場合の数の使い分け（その２）
解答１．（ア）(1) 64 (2) 32 (3) 7 (4) 4 （イ）(1) 62 (2) 31 (3) 5 (4) 3
解説（ア）
(1) （重複順列）
玉は区別できるので、a, b, c, d, e, f と名前がついているとする。また、箱も区別できるので、X, Yと名前がついているとする。
a をX, Yのどちらに入れるかで2通り、以下 b から f も同様に2通りずつあるから、
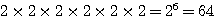通り
(2) （重複順列）
まず(1)と同じように、とりあえず箱に名前がX, Yがついているとして数えると、(1)の64通り。その中で、左が箱X、右が箱Yとして、
(a, b, c) (d, e, f) と (d, e, f) (a, b, c)
(a, b, c, d) (e,
f) と (e, f) (a, b, c, d)
(a, b, c, d, e) (f) と (f) (a, b, c,
d, e)
(a, b, c, d, e, f) () と () (a, b, c, d, e, f)
・・・など、ちょうど2組ずつが、箱の名前の付け方が異なるだけで、分かれ方が同じである。したがって(1)で数えたものを2!=2組ずつ一まとめにすると考えればよく、答えは、
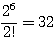通り
(3) （重複組合せ） 今度は玉が区別できないので、順列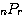
, 
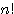組合せ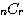
は使えない。
6個の同じ○と、2種類の箱X, Yに分けるための仕切り｜1個を一列に並べると考える。
○○○○○○｜
同じものを含む順列の考え方で、答えは、
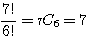通り
仕切りより左が箱Xに入る個数、右は箱Yの個数と考える。たとえば、
○○｜○○○○ ならば、Xに2個、Yに4個
｜○○○○○○ ならば、Xに0個、Yに6個
ということである。
(4) （地道に数える） さらに箱も区別できなければ、分かれ方を地道に数え上げるしかない。
(6, 0) (5, 1) (4, 2) (3, 3) の4通り
（イ） どの箱にも少なくとも1個の玉が入るので、「（ア）で数えたものから何も入っていない箱を除く」と考えるのが基本。
(1) （重複順列） （ア）(1)で数えた64通りから、「すべての玉が箱Xに入る」「すべての玉が箱Yに入る」の2通りを引くと考えればよく、答えは
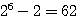通り
(2) （重複順列）（イ）(1)で求めた62通りを、（ア）(2)と全く同様に、2組ずつ一まとめにすると考えて、答えは
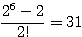通り
(3) （重複組合せ） （ア）(3)と全く同様に、6個の同じ○と、2種類の箱に分けるための同じ仕切り｜1個を用意する。ただし0個の箱があってはならないから今度は、○だけ一列に並べておき、その両端を除いたスキマに仕切り｜1個を入れる入れ方を考える。
○∧○∧○∧○∧○∧○ ← ｜
上のスキマ∧のうちに1つに対し、最高1個｜を入れる入れ方を考える。5個の∧から｜を入れる∧1個を選べばよく、答えは、
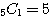通り
(4) （地道に数える） これも（ア）(4)と同様に、分かれ方を地道に数え上げるしかない。
(5, 1) (4, 2) (3, 3) の3通り
******************************************************************
※（ア）(1)は次のように考えることもできる。
箱Xに入る玉の個数は 6個 または 5個 または ・・・ または 0個 だから、
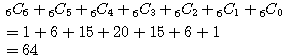
ちなみにこれは、二項定理
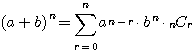
で、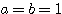
としたものになっている。
******************************************************************
重複順列、重複組合せという言葉が登場した。単なる「順列」「組合せ」との違いをしっかりつけられるようにしようという意味で、筆者は「選ぶ（並べる）物の使用回数に制限があるか否か」と「並べるのか選ぶのか」に注意しようと言うことがある。
|
|
並べる |
選ぶ |
|
使用回数の制限あり |
順列 |
組合せ |
|
使用回数の制限なし |
重複順列 |
重複組合せ |
「選ぶものの使用回数」について、次の具体例をよく読んで違いを理解してほしい。
◎使用回数が決まっているものの例
(1) 10個の異なる色の玉から3個を取り出して並べる
(2) 10人の人から4人を選ぶ
など、そもそもすべてが異なるものを選ぶ（並べる）場合。一つ一つが一回ずつしか使えないため。(1)は並べるので順列
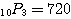通り、(2)は選ぶだけなので組合せ 
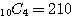通り。
(3) 赤球2個・白球3個・青球4個を一列に並べる
など、同じものが何個かずつあっても、それをすべて使う場合。同じ物を含む順列の考え方で、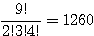
通り。
◎使用回数が決まっていないものの例
(1) 1, 2, 3の数字を繰り返し用いて5桁の整数を作る
(2) りんご・みかん・ぶどうがたくさんあり、5つの果物入りの箱を作る
など、回数の上限に制限がない場合。(1)は並べるので重複順列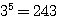 
通り、(2)は重複組合せで、使わない果物があってもいいなら （ア）(3)と同じ考えで
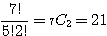通り。どの果物も必ず1つは使うならば（イ）(3)と同じ考え方で 
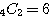通り。
難しいのは、「同じものが何個かずつあるのに、それをすべて使うわけではない場合」である。例えば「赤球2個・白球3個・青球4個のうちから5個を選んで一列に並べる」など。こういった場合、
（ｉ）まず何を使うか選び （ｉｉ）その後で並べる
というように順を追って考えていくのがよい。
以下、選んだ玉の個数を(赤, 白, 青)で表す。それらの並べ方の場合の数を、→の後ろで計算した。
（ｉ）選ぶ （ｉｉ）並べる
(0, 1, 4) →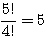 
(0, 2, 3) →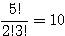 
(0, 3, 2) →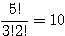 
(1, 0, 4) →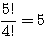 
(1, 1, 3) →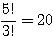 
(1, 2, 2) →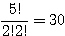 
(1, 3, 1) →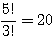 
(2, 0, 3) →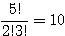 
(2, 1, 2) →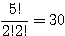 
(2, 2, 1) →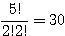 
(2, 3, 0) →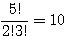 
したがって、5+10+10+5+20+30+20+10+30+30+10=180 通り。
ということで次は、 「順列」「組合せ」「重複順列」「重複組合せ」の4つについて、もう少し詳しく考えてみよう。
Copyright (C) 2004- imasen, All rights reserved.