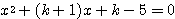・・・(*)イマセン第16回 条件をそろえよう〜２〜
とりあえず、模範解答は次の通りである。
********************************************************************
方程式
・・・(*)
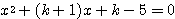において、まず、実数解を持つことが条件だから、(*)の判別式を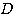
とすると、
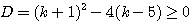よって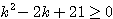 
左辺を変形して、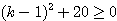
これはすべての実数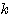
に対して成り立つので、
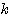がどのような値をとっても(*)は必ず実数解を持つ。
このとき、(*)の2つの実数解を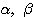
とすると、
解と係数の関係より、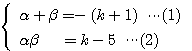
また、一つの解が他の解の平方より、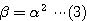
（これは
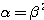でもよい）
ここで(3)を(1)(2)に代入して、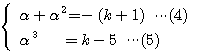
(4)+(5)より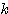
を消去して、 
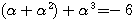すなわち、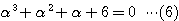
(6)は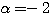 
を解に持つことが分かるので、因数定理を用いて(6)の左辺を因数分解すると、
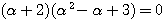
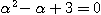の判別式を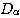
とすると、
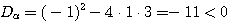
となって実数解を持たないので、(6)の実数解は、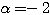
のみ。
(3)より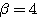
であり、これと(1)または(2)より、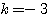
よって、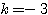
・・・（答）
********************************************************************
さて、今回のテーマは条件をそろえようである。〜３〜では、この解き方で特に注意してほしい箇所を見てみよう。
Copyright (C) 2004- imasen, All rights reserved.