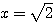のとき、最小値 4 イマセン第18回 忘れた頃にやってくる最大・最小 〜その２〜
解答 (1) 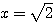のとき、最小値 4
解説
(1) 分数式の最大・最小の場合、まずは分母と分子の次数を見よう。
もしも(分子の次数)≧(分母の次数)ならば、どんなときでも、割り算をして(分子の次数)＜(分母の次数)にしてから考える。
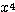を 
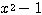で割ると、商 
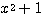，余り 1 であるから、
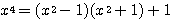← (割られる式)＝(割る式)×(商)＋(余り)
∴ 
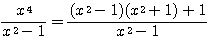← 両辺を 
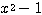で割った
∴ 
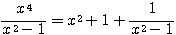
したがって関数は、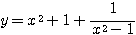
・・・(*) と変形できる。
この最小値を求めるために、もしも数学３まで学んでいる人なら微分を用いればよいが、１２ABまでしか学んでいない人でも以下のようにできる。その方法は、実は微分を用いるより計算が楽である。
そこでまず、次のような事実を思い出そう。
＜相加平均・相乗平均の関係式＞
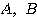を 0 以上の数とするとき、常に 
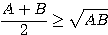が成り立つ。
等号は、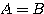
のときに成り立つ。
※ただし実際にこれを利用する場合は、分母を払って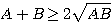 
として使うことが多い。
（使用例）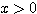 
のとき、関数 
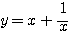の最小値とそのときの 
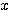の値
（方針）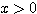 
，
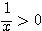であるので、
，
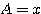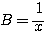として相加相乗を用いる。
（解）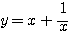 
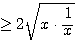
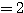であるから、つねに 
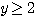である。
等号は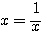 
すなわち 
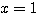のときに成り立つ。
したがって、最小値は 2 であり、このとき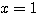 
である。
使用例のポイントは、積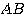 
を計算すると文字が約分されて消えるところにある。そこに注意しておこう。
さていよいよ
・・・(*)
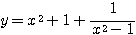であるが、お察しの通り「相加相乗」を用いる。ただし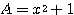 
，
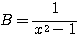としても 積 
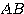に文字が残ってしまうので、用いる前に一工夫必要である。
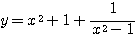
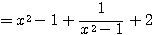← 分母にあわせて、
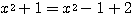とした。
← 
，
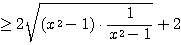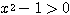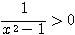より、相加相乗を用いて、
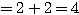
等号は、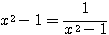
すなわち 
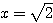のときに成立。
したがって、最小値は 4 であり、このとき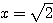 
である。
分母にあわせて、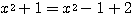
とするところがポイントである。
Copyright (C) 2004- imasen, All rights reserved.