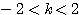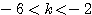
イマセン第17回　条件を言い換える〜２〜

解答１．　(1)　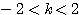　　(2)　

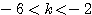
解説１．

　2次方程式や2次不等式は、2次関数のグラフで考える。グラフが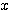 軸と交点を何個持つかにより、解が変わってくる。そこで登場するのが「判別式」である。

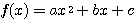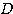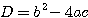　2次関数 について、判別式 を  と定める。

　この判別式 の符号により、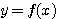 のグラフと 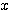軸との位置関係が変わってくる。

　（ア）　 のとき、グラフは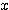 軸と異なる2点で交わる。
　（イ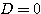）　 のとき、グラフは 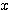軸と1点で交わる（接する）。
　（ウ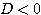）　 のとき、グラフは 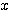軸と交わらない。

　これを利用して、問題を解いていこう。

(1)　2次不等式　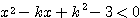　が解を持つためには、

　　2次関数 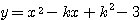が 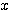軸と異なる2点で交わればよいから、条件は である。

　※上図の太線部にある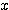 が解。（ア）の場合のみ解が存在する。

　　
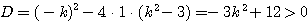
　　これを解いて、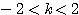

(2)　2次不等式　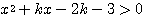　の解がすべての実数であるためには、

　　2次関数 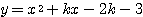が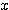 軸と交わらなければよいから、条件は 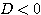である。

　※上図の太線部にある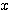 が解。（ウ）の場合のみすべての実数が解である。

　　
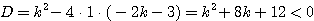
　　これを解いて、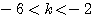

その３（解答編）へ

その１（問題編）へ

イマセンTOPへ

Copyright (C) 2004- imasen, All rights reserved.