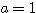 ,
, 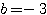 ,
, 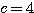
イマセン第9回 連立方程式を解く<1>〜その2〜
解答
(1) 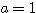 ,
, 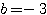 ,
, 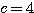
解説
(1) 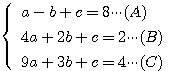
連立方程式の基本「消去法」
基本は、「特定の文字に注目し、まずその文字だけを消す」ということだ。この「特定の文字に注目」ということを忘れると、堂々巡りがおき、一向に連立方程式が解けない。
どんな組み合わせでもいい、とにかく式を2つずつ組み合わせ、まず両方から同じ文字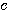 を消去する。別にそれはほかの文字でも良いのだが、この問題は
を消去する。別にそれはほかの文字でも良いのだが、この問題は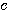 がいちばん消去しやすい。
がいちばん消去しやすい。
なぜなら、(A)(B)(C)の3式における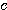 の係数はすべて1であり、単に辺々引き算するだけで、すんなりと
の係数はすべて1であり、単に辺々引き算するだけで、すんなりと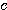 が消去できるからだ。
が消去できるからだ。
(A)-(B)より、
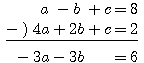 したがって両辺を-3で割り、
したがって両辺を-3で割り、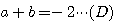
また(B)-(C)より、
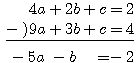 したがって、
したがって、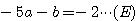
さて、このようにして得られた(D)(E)から、今度はまた別の文字を消去していく。
(D)+(E)より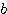 を消去し、
を消去し、
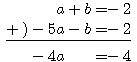 したがって両辺を-4で割り、
したがって両辺を-4で割り、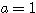
一つでも値が出れば、後は代入していくだけ。
(D)に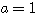 を代入して、
を代入して、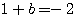 。したがって、
。したがって、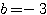 。
。
また、(A)に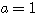 、
、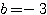 を代入して、
を代入して、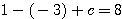 。したがって、
。したがって、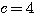 。
。
Copyright (C) 2004- imasen, All rights reserved.