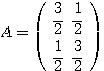 とする。次の各問いに答えよ。
とする。次の各問いに答えよ。直交行列による対称行列の対角化(その4)
最後に、大学入試問題である。
(問題) 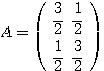 とする。次の各問いに答えよ。
とする。次の各問いに答えよ。
(1) 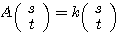 が成り立つような実数
が成り立つような実数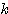 の値を2つ求めよ。ただし、
の値を2つ求めよ。ただし、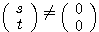 とする。
とする。
(2) (1)で求めた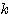 の値を
の値を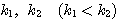 とし、
とし、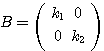 とする。このとき、
とする。このとき、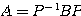 を満たし、かつ
を満たし、かつ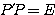 となる
となる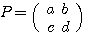
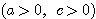 を求めよ。ただし、
を求めよ。ただし、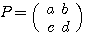 に対して
に対して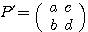 であり、
であり、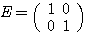 である。
である。
(01 名古屋大/後期 の一部)
まさしく、対称行列の対角化が話題になっている。
行列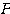 を直交行列となるように作れば、それは自動的に(その3)の性質1を満たすので、(2)の”かつ〜”以降は本来不要である。これは直交行列の性質を知らなくても、成分計算だけで行列
を直交行列となるように作れば、それは自動的に(その3)の性質1を満たすので、(2)の”かつ〜”以降は本来不要である。これは直交行列の性質を知らなくても、成分計算だけで行列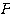 が求められるようにするためのヒントである。その解き方は赤本や問題集等を参考にしてほしい。
が求められるようにするためのヒントである。その解き方は赤本や問題集等を参考にしてほしい。
ここでは先ほどまでと同じように、行列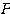 を直交行列となるように作ることにする。
を直交行列となるように作ることにする。
ただし、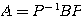 より
より 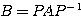 であるので、
であるので、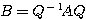 を満たす直交行列
を満たす直交行列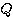 を作り、
を作り、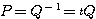 とおけばよい。
とおけばよい。
(解)
(1) 行列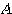 の固有値を求めよという問題であある。
の固有値を求めよという問題であある。
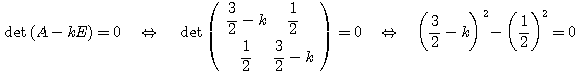
を解いて、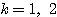 したがって固有値は、
したがって固有値は、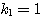 ,
,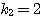 ・・・(答)
・・・(答)
(2) 行列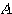 の固有ベクトルで絶対値が1となるものを求める。
の固有ベクトルで絶対値が1となるものを求める。
(i)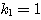 のとき
のとき
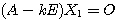 すなわち
すなわち 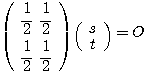 ここから、特に
ここから、特に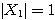 となるものを選べば、
となるものを選べば、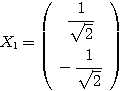
(ii)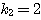 のとき
のとき
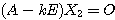 すなわち
すなわち 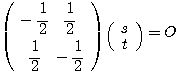 ここから、特に
ここから、特に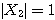 となるものを選べば、
となるものを選べば、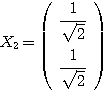
したがって、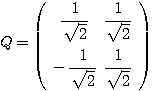 とおき、
とおき、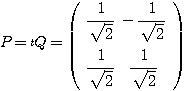 ・・・(答)
・・・(答)
よって、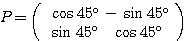 と、回転行列の形となる。
と、回転行列の形となる。
ちなみにこの入試問題の続きは次のようになっている。
(3) 実数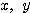 に対して、
に対して、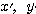 を
を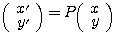 で定める。点
で定める。点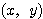 が円
が円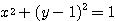 の上を動くとき、点
の上を動くとき、点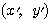 の軌跡を図示せよ。
の軌跡を図示せよ。
(4) すべての実数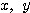 に対して、
に対して、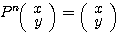 となる最小の自然数
となる最小の自然数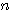 を求めよ。
を求めよ。
(解) 行列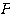 は
は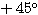 回転の行列だと分かっているから、(3)(4)はほとんど暗算である。
回転の行列だと分かっているから、(3)(4)はほとんど暗算である。
(3) 与えられた円は中心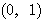 ・半径1である。回転するだけでは長さが変わらないから、中心は
・半径1である。回転するだけでは長さが変わらないから、中心は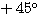 回転され
回転され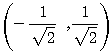 、半径は1のまま。
、半径は1のまま。
求める軌跡は、円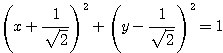 ・・・(答) (図は省略する)
・・・(答) (図は省略する)
(4) 回転行列について、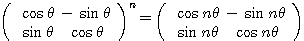 という非常にキレイな性質があった(注)
という非常にキレイな性質があった(注)
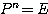 より、
より、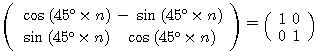 すなわち
すなわち 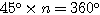 より
より 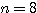 ・・・(答)
・・・(答)
自分が大学で線型代数を学んだとき(とはいっても授業にはほとんど出ず、本で勉強していたのだけれど)、「一般の 次元での議論」など抽象的な話が多くて、あまりイメージがわかなかった。
次元での議論」など抽象的な話が多くて、あまりイメージがわかなかった。
もっとも、そんなことも軽くクリアしてしまうような人がきっと学者になるんだろうけれど、でも自分は、2次元とか3次元とか、目で見えて分かりやすい例がもう少しでいいからあればいいのに、と思っていた。それが一般の学生の正直なところなのではないだろうか。
Copyright (C) 2004- imasen, All rights reserved.