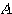 を対称行列としたのはなぜか。
を対称行列としたのはなぜか。直交行列による対称行列の対角化(その3)
さて、得られた結論は非常にきれいなものだったが、次のような疑問が起こる。
1.行列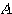 を対称行列としたのはなぜか。
を対称行列としたのはなぜか。
2.行列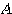 を対角化するとき、固有ベクトルを絶対値が1になるようなものとして選んだのはなぜか。行列
を対角化するとき、固有ベクトルを絶対値が1になるようなものとして選んだのはなぜか。行列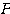 が回転行列になったのはなぜか。
が回転行列になったのはなぜか。
1.について
行列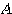 が対称行列であるとき、その2つの固有ベクトルは直交する。普通はなかなか技巧的に証明するが、ここでは2次の場合についてのみ考えるので、地道に次のような計算で証明しようと思う。
が対称行列であるとき、その2つの固有ベクトルは直交する。普通はなかなか技巧的に証明するが、ここでは2次の場合についてのみ考えるので、地道に次のような計算で証明しようと思う。
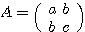 より、
より、
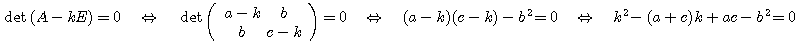 ・・・(3.1)
・・・(3.1)
の解が固有値である。まず(*)の判別式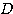 について、
について、
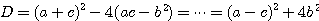
なので、行列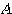 が単位行列の実数倍にならない限り
が単位行列の実数倍にならない限り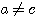 または
または 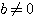 なので、
なので、 。すなわち(3.1)は異なる2つの実数解をもつ。
。すなわち(3.1)は異なる2つの実数解をもつ。
このもとで(3.1)の2実解(固有値)を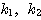 とおく。
とおく。
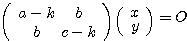 となるので、各固有値に対する固有ベクトルを、
となるので、各固有値に対する固有ベクトルを、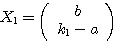 ,
,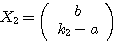 とすればよい。
とすればよい。
このとき2ベクトルの内積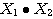 について、
について、
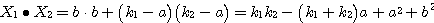 ・・・(3.2)
・・・(3.2)
となるが、ここで(3.1)において解と係数の関係より 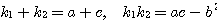 なので、(3.2)に代入し、
なので、(3.2)に代入し、
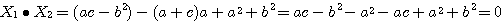
したがって内積が0なので、対称行列の2つの固有ベクトルは直交する。直交することで何が良いのか、というのは2.以降の話へとつながる。
2.について
2つの固有ベクトル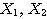 は必ず直交する。そしてそれらの固有ベクトルの実数倍もまた固有ベクトルであるから、とくに絶対値が1となるものを選ぶことができる。そのように作られた行列
は必ず直交する。そしてそれらの固有ベクトルの実数倍もまた固有ベクトルであるから、とくに絶対値が1となるものを選ぶことができる。そのように作られた行列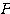 は、次のような性質を満たす。
は、次のような性質を満たす。
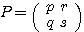 ただし
ただし 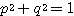 ,
,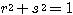 ,
,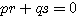 ・・・(3.3)
・・・(3.3)
そしてこの(3.3)を満たす行列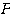 を直交行列といい、さらに次のような性質をもつ。
を直交行列といい、さらに次のような性質をもつ。
(性質1) 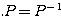 すなわち
すなわち 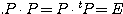 である(注)。
である(注)。
(性質2) とくに成分をすべて実数に限ると、 は原点の周りの
は原点の周りの 回転を表す行列
回転を表す行列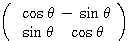 、または原点を通る直線
、または原点を通る直線 に関する対称移動を表す行列
に関する対称移動を表す行列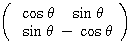 の形となる。
の形となる。
これらの性質を証明してみよう。
(性質1の証明) 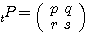 および
および 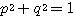 ,
,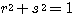 ,
,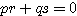 より
より
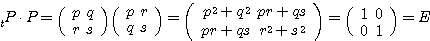 ■
■
(性質2の証明) 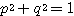 より
より 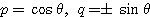 ,
,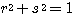 より、
より、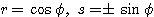 とおける。
とおける。
(1) 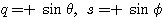 の場合
の場合
このとき 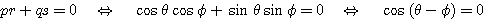
であるから、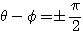 でなければならない。
でなければならない。
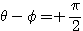 のとき
のとき 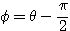 より
より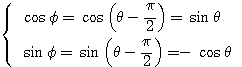 であるから、
であるから、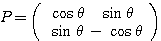 とおける(対称移動)。
とおける(対称移動)。
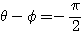 のとき
のとき 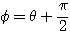 より
より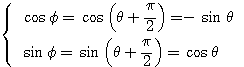 であるから、
であるから、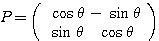 とおける(回転移動)。
とおける(回転移動)。
(2) 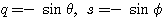 の場合
の場合
このとき 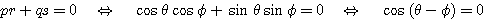
であるから、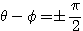 でなければならない。
でなければならない。
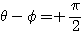 のとき
のとき 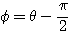 より
より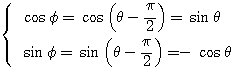 であるから、
であるから、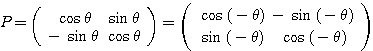 とおける(回転移動)。
とおける(回転移動)。
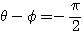 のとき
のとき 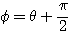 より
より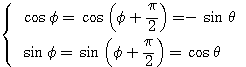 であるから、
であるから、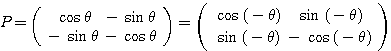 とおける(対称移動)。
とおける(対称移動)。
(3) 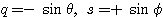 の場合
の場合
このとき 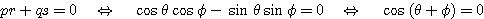
であるから、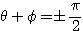 でなければならない。
でなければならない。
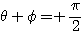 のとき
のとき 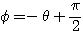 より
より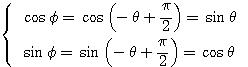 であるから、
であるから、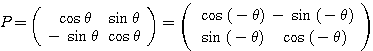 とおける(回転移動)。
とおける(回転移動)。
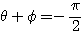 のとき
のとき 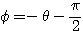 より
より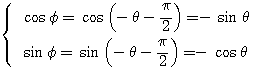 であるから、
であるから、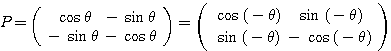 とおける(対称移動)。
とおける(対称移動)。
(4) 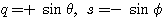 の場合
の場合
このとき 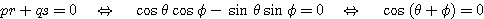
であるから、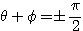 でなければならない。
でなければならない。
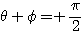 のとき
のとき 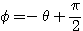 より
より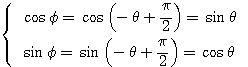 であるから、
であるから、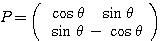 とおける(対称移動)。
とおける(対称移動)。
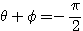 のとき
のとき 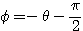 より
より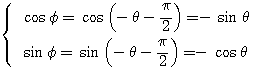 であるから、
であるから、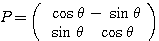 とおける(回転移動)。
とおける(回転移動)。
長くなってしまったが(もしかするともっと短く出来るかも)結果は綺麗である。固有ベクトルの絶対値をわざわざ1にしたのは、行列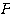 を、性質の非常にキレイな直交行列にしたいからであった。
を、性質の非常にキレイな直交行列にしたいからであった。
したがってその2における<fact>を少し言い換えると、次のようになる。
<fact>
対称行列は、直交行列(とくに成分がすべて実数であるとき、回転移動または対称移動を表す行列)により対角化できる。
Copyright (C) 2004- imasen, All rights reserved.