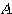 は対角化されて行列
は対角化されて行列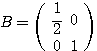 になった。そこでとりあえず
になった。そこでとりあえず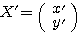 として、行列
として、行列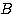 により表現される二次曲線
により表現される二次曲線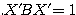 がどのようなものなのかを考えてみる。
がどのようなものなのかを考えてみる。直交行列による対称行列の対角化(その2)
Step2 行列Bによって表現される二次曲線
行列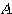 は対角化されて行列
は対角化されて行列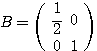 になった。そこでとりあえず
になった。そこでとりあえず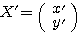 として、行列
として、行列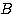 により表現される二次曲線
により表現される二次曲線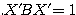 がどのようなものなのかを考えてみる。
がどのようなものなのかを考えてみる。
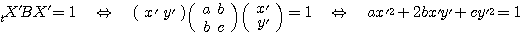
であったから、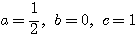 すなわち
すなわち 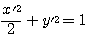 となり、これは焦点
となり、これは焦点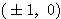 ,長軸
,長軸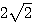 ,短軸2の楕円の標準形である。行列
,短軸2の楕円の標準形である。行列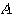 が対角化できた(
が対角化できた(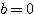 とできた)ことで、二次曲線の特徴が非常に良く捉えられた。
とできた)ことで、二次曲線の特徴が非常に良く捉えられた。
Step3 行列Aによって表現される二次曲線
さらに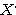 と
と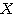 との関係を求めよう。
との関係を求めよう。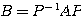 であったことより
であったことより
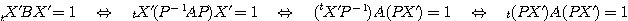
となる。ただし3番目から4番目への変形は、
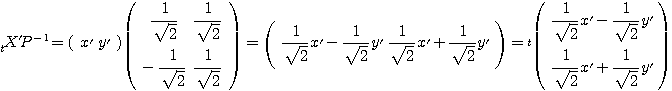
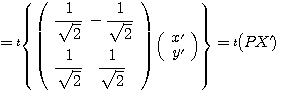
であることによる。この変形により、
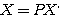
であるといえて、さらにこの式により、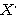 の世界で基本のベクトルである
の世界で基本のベクトルである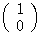 と
と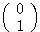 が、
が、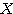 の世界ではどのようなベクトルなのかが分かる(注)。
の世界ではどのようなベクトルなのかが分かる(注)。
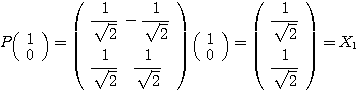 ,
, 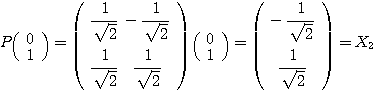
すなわち、Step1で求めた2つの固有ベクトル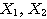 そのものを基本のベクトルとして、新たな座標軸と考えたということである。この新たな座標軸のもとでは、二次曲線は
そのものを基本のベクトルとして、新たな座標軸と考えたということである。この新たな座標軸のもとでは、二次曲線は によって表される。
によって表される。
Step4 行列Pの特徴
最後に行列Pの特徴について考えよう。
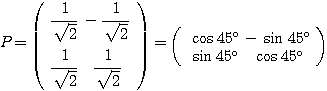
と書ける。これは、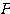 が原点を中心とした
が原点を中心とした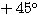 の回転移動であることを表している。
の回転移動であることを表している。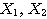 を
を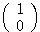 と
と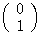 とみなす、ということは座標軸が
とみなす、ということは座標軸が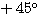 回転したということである。
回転したということである。
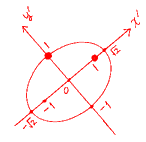 →
→ 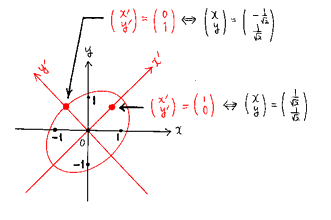
したがってStep3で得られた事実を言い換えれば、楕円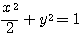 を原点を中心に
を原点を中心に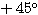 回転させれば、二次曲線
回転させれば、二次曲線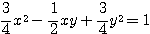 を表す、ということである。そしてその
を表す、ということである。そしてその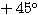 とは、行列
とは、行列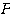 を作ることで分かってしまう。実質、行列
を作ることで分かってしまう。実質、行列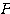 を作った時点で2次曲線の特徴が、「回転」という非常に視覚的な操作によりきちんと捉えられる、ということなのだ。
を作った時点で2次曲線の特徴が、「回転」という非常に視覚的な操作によりきちんと捉えられる、ということなのだ。
実は、以下のfactが成り立つ。
<fact>
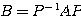 として対称行列
として対称行列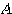 を対角化したとする。このとき、
を対角化したとする。このとき、
●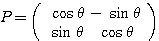 と、回転行列の形に表すことができる。
と、回転行列の形に表すことができる。
●二次曲線 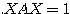 は、原点を中心に標準形
は、原点を中心に標準形 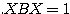 をθだけ回転させたものである。
をθだけ回転させたものである。
Copyright (C) 2004- imasen, All rights reserved.