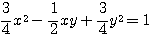…(*)により表される図形を考えてみよう。これは
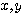の2次式だから、一般には二次曲線と言われる「楕円」「双曲線」「放物線」のどれかを表すはずである。ところが、
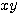の項が邪魔してどれなのかを分かりづらくしている。ここでは行列を用いて、どのような二次曲線を表すのかを考えてみよう。以下、文字はすべて実数を表すものとする。直交行列による対称行列の対角化（その１）
高校の数学Cで習う「行列」という単元と、大学１年で学ぶ「線型代数」には、同じ「行列」について学ぶ分、密接な関係がある。ただ高校範囲ではほとんど計算だけで答えが出せる分本質が見えないし、大学では抽象的なことが多くていまいちイメージがわかない。今回はその２つの橋渡しが少しでもできればよいなと思う。
高３数学C「行列」「二次曲線」の教科書内容を一通り学んだ人向けである。（注）はその用語の説明や関連内容です。
方程式 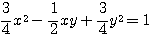…(*)により表される図形を考えてみよう。これは 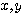の2次式だから、一般には二次曲線と言われる「楕円」「双曲線」「放物線」のどれかを表すはずである。ところが、 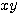の項が邪魔してどれなのかを分かりづらくしている。ここでは行列を用いて、どのような二次曲線を表すのかを考えてみよう。以下、文字はすべて実数を表すものとする。
2次の対称行列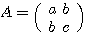
（すなわち対角成分を境に右上と左下が対称的）を用いて、一次の項を持たない任意の二次曲線が
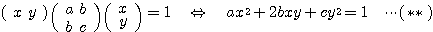
と表せる。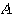
が対称行列でなくても表せるのだが、対称行列にしておくことで、後述するように理論的に非常にきれいになる。
また、特にベクトル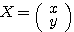
を用いることによって、
と表せることにも注意しておく（注）
さて、(*)(**)の係数を比較して
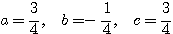
となる。二次曲線(*)の特徴を捉えるために、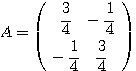
として、まずは行列
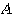を対角化（注）することを考える。対角化のためにはStep1のように、固有ベクトルを利用する。
Step1 行列Aの対角化
１． 固有値を求める
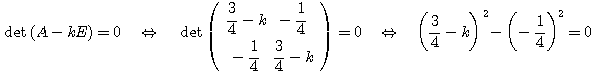
これを解いて、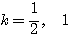
２． 固有ベクトルを求める
(i)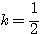
のとき
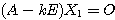すなわち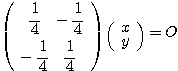 
ここから、特に
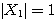となるものを選べば、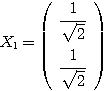
(ii)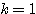
のとき
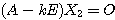すなわち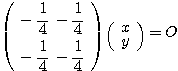 
ここから、特に
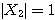となるものを選べば、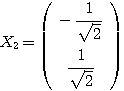
３． 対角化する
２．で得られた2つのベクトル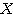
を左右に並べてできる2次正方行列
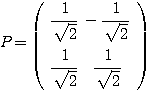を作れば、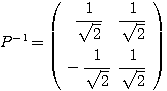
であることより、
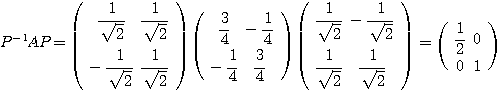
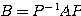とおくことにより、行列
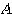は対角化されて行列
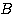になった（注）。これを用いて二次曲線(*)の特徴をその２以降で捉えていこう。
Copyright (C) 2004- imasen, All rights reserved.