 (
(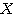 の転置行列)
の転置行列)直交行列による対称行列の対角化 用語集
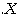 のような"t"の記号について(本来ならば左上につくが、このページを作成しているソフトの事情により左下にしかつけられないようだ)は、行列(ベクトル)の「転置」を表す。転置とは「
のような"t"の記号について(本来ならば左上につくが、このページを作成しているソフトの事情により左下にしかつけられないようだ)は、行列(ベクトル)の「転置」を表す。転置とは「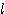 行
行 列行列を、
列行列を、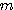 行
行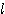 列行列にし」、「
列行列にし」、「 成分を
成分を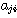 成分にする」ことである。
成分にする」ことである。
(例) 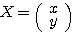 ならば
ならば  ,
, 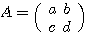 ならば
ならば 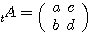 ,
, 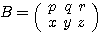 ならば
ならば 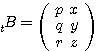
2次正方行列で、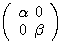 のように左上から右下にかけての成分(対角成分)以外は0である行列を、対角行列という。行列
のように左上から右下にかけての成分(対角成分)以外は0である行列を、対角行列という。行列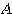 に対してうまい行列
に対してうまい行列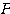 が見つかって、
が見つかって、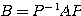 をみたす行列
をみたす行列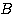 が対角行列になったとき、行列
が対角行列になったとき、行列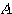 は行列
は行列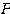 によって行列
によって行列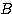 に対角化された、という。
に対角化された、という。
一般の行列の積ではきれいな規則は何もないが、対角行列の場合
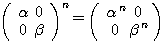
という非常に単純な規則がある(2乗、3乗と具体的に計算していくと分かる)。つまり対角行列に変形できれば、積の計算の煩わしさを回避できるというメリットがあるのだ。だから、行列は何とか苦心して対角化することをまず考える。大学入試の話題としても多い。
行列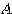 に対して、実数
に対して、実数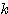 およびベクトル
およびベクトル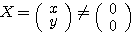 が、方程式
が、方程式
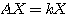
を満たすとする。このときの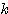 を行列
を行列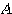 の固有値、
の固有値、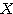 を(各
を(各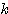 に対する)固有ベクトルという。各行列に対してそれらを具体的に求める方法は、(その1)で示したとおりである。
に対する)固有ベクトルという。各行列に対してそれらを具体的に求める方法は、(その1)で示したとおりである。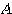 が2次の正方行列の場合、一般的には固有値が2つ存在する(
が2次の正方行列の場合、一般的には固有値が2つ存在する(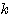 の2次方程式となるので)。ここではさらに深く突っ込んで、次の定理を紹介しよう。
の2次方程式となるので)。ここではさらに深く突っ込んで、次の定理を紹介しよう。
(定理) 2次正方行列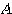 の2つの固有値を
の2つの固有値を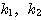 とし、それぞれに対する固有ベクトルを
とし、それぞれに対する固有ベクトルを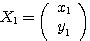 ,
,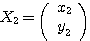 とする。さらに
とする。さらに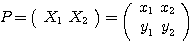 とする。このとき、
とする。このとき、
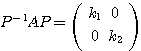
が成り立つ(行列 が行列
が行列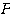 により対角化でき、さらにその対角成分は行列
により対角化でき、さらにその対角成分は行列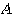 の2つの固有値である)。
の2つの固有値である)。
(証明)
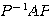 の第1列と第2列に分けて考える。
の第1列と第2列に分けて考える。
第1列: 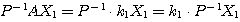 ・・・(*)
・・・(*)
ここで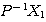 は
は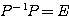 の第1列なので、
の第1列なので、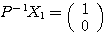
したがって、(*)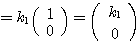
第2列: 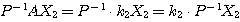 ・・・(**)
・・・(**)
ここで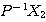 は
は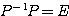 の第1列なので、
の第1列なので、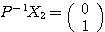
したがって、(*)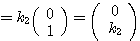
以上より、 となる。
となる。
<基底>
Oを原点とする座標平面上に2つのベクトル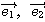 があり、ベクトル
があり、ベクトル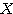 を
を
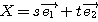 ・・・(*)
・・・(*)
とおく。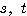 がすべての実数を動くとき、
がすべての実数を動くとき、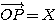 によって表される点Pが座標平面上のすべての点を表すことができるならば、2つのベクトルの組
によって表される点Pが座標平面上のすべての点を表すことができるならば、2つのベクトルの組 を(座標平面の)基底という。特に座標平面では、一次独立な(=ともに零ベクトルではなく、互いに平行ではない)2つのベクトルの組はすべて基底である。
を(座標平面の)基底という。特に座標平面では、一次独立な(=ともに零ベクトルではなく、互いに平行ではない)2つのベクトルの組はすべて基底である。
(例1)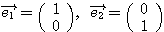 のとき、
のとき、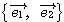 は最も標準的な基底である。このときPの座標は
は最も標準的な基底である。このときPの座標は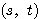 である。
である。
(例2)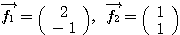 のときも、
のときも、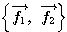 は一次独立なので基底である。
は一次独立なので基底である。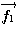 を1目盛とする
を1目盛とする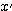 軸、
軸、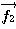 を1目盛とする
を1目盛とする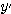 軸を取れば、
軸を取れば、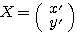 と考えることができる。この座標軸を(座標軸が直交する直交座標という言葉に対して)座標軸が斜めに交わる斜交座標とよぶこともある。
と考えることができる。この座標軸を(座標軸が直交する直交座標という言葉に対して)座標軸が斜めに交わる斜交座標とよぶこともある。
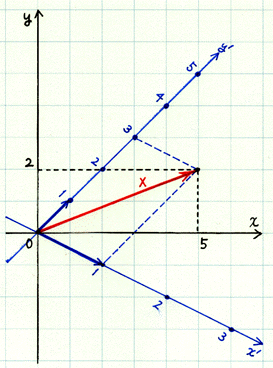
※(例1)の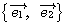 、(例2)の
、(例2)の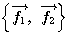 に対し、同じベクトル
に対し、同じベクトル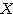 が
が 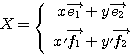 とそれぞれ表されているとする。
とそれぞれ表されているとする。
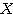 が図のようなベクトルの場合、
が図のようなベクトルの場合、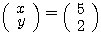 ,
,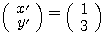 である。同じベクトル
である。同じベクトル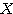 でも基底の取り方によって成分表示の方法はいろいろある。
でも基底の取り方によって成分表示の方法はいろいろある。
(例3)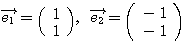 のときは、
のときは、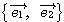 は
は 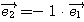 を満たすので一次独立ではないから、基底ではない。
を満たすので一次独立ではないから、基底ではない。
図形的に言えば、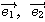 がともに同じ
がともに同じ 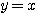 という直線上にあるので、どのように実数
という直線上にあるので、どのように実数 を取っても、点Pは直線
を取っても、点Pは直線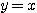 上にしか存在しないということである。
上にしか存在しないということである。
<基底の取替え>
座標平面上の2つの異なる基底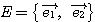 ,
,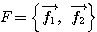 に対して、同じベクトル
に対して、同じベクトル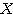 が
が
 ・・・(**)
・・・(**)
とそれぞれ表されているとする。このときある行列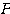 が存在して、(**)を満たすどのような
が存在して、(**)を満たすどのような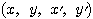 の組に対しても、
の組に対しても、
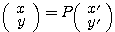
と表せることが知られている。この行列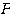 を
を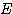 から
から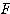 への基底の取替え行列という。
への基底の取替え行列という。
特に基底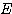 のベクトルを
のベクトルを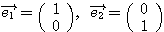 とし、基底
とし、基底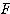 のベクトルを
のベクトルを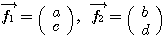 とするならば、
とするならば、
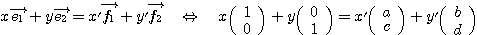
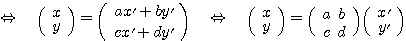
であるから、基底の取替え行列は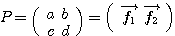 である。
である。
したがって(その2)における 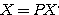 という関係式も、基底の2ベクトル
という関係式も、基底の2ベクトル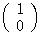 と
と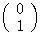 が、それぞれ
が、それぞれ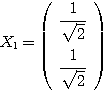 と
と に変わった、ということを示している。このとき、
に変わった、ということを示している。このとき、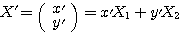 として二次曲線を
として二次曲線を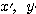 で表現したとき、標準形で表すことができるということである。
で表現したとき、標準形で表すことができるということである。
行列 が直交行列ならば、つねに
が直交行列ならば、つねに  が成り立つ。
が成り立つ。
(証明) 1番目から2番目への変形は、(その3)における直交行列の性質その1による。
2番目から3番目への変形は、
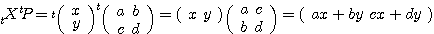
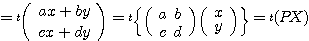
であることによる。
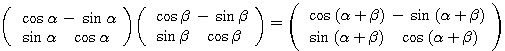
となることが証明できればよい(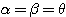 とすれば2乗の場合が示せて以下同様)。
とすれば2乗の場合が示せて以下同様)。
(式変形による証明) 左辺の積を実際に計算すると
(左辺)=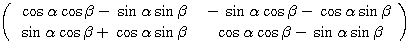
となり、各成分に三角関数の加法定理を用いれば右辺になる。
(図形的な証明) 左辺は、まずβ回転させ、次にα回転させる操作である。これは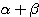 回転させることに他ならないので、右辺に等しい。
回転させることに他ならないので、右辺に等しい。
Copyright (C) 2004- imasen, All rights reserved.