トレミーの定理の証明～３～

ところで、こんな問題がある。

　問題　一辺の長さが1である正五角形ABCDEの対角線の長さを求めよ。

　正攻法では、三角形の相似を使えば解けるが、相似であることを証明するのが意外と面倒くさかったりする。

正五角形

　正五角形の一つの角の大きさは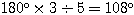であり、上図において△ABCや△ABEはその角を頂角に持つ二等辺三角形だから、残りの角は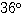ずつとなる。　したがって、2角相等により △ABC∽△AFB すなわち AB:AC=AF:AB　・・・(1)

　一方、△CBFがCB=CF=1の二等辺三角形となることより、対角線の長さを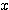とおけば、(1)より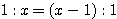

　よって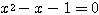が成り立ち、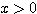より　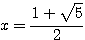・・・（答）

　ところが、生徒の一人がこの問題をトレミーの定理を使って解いていた。

円に内接する正五角形

　一般に正n角形は円に内接し、さらに上図における四角形ABCD（太線部）もまた、円に内接する四角形となる。

　したがって、対角線の長さ AC=AD=BD=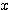 とし、四角形ABCDにトレミーの定理を用いれば、

　　AB・CD+AD・BC=AC・BD　すなわち　

　が成り立つ。これは正攻法で得られた方程式と同じであるから、　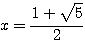・・・（答）

　生徒のその発見に、なるほどと膝を打った。