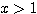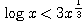
極限の強弱の証明　〜その６〜　考察

　求められた不等式

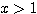　　　　のとき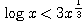　

は、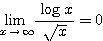 の証明の際に、決して一般的に使われるものではないだろう。きっと何か背景があって 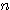がどのような正の値でも、

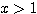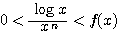　　　　のとき　，　かつ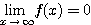　

　となる 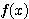がもしかしたら存在するのかもしれない。筆者は不勉強なので今の所それが分からないのだが、その上で何とか証明してみようというのは、受験生と同じ立場になるということで、勉強になったと思う。

　これを質問に来た当の本人は、証明を見せたら満足して去っていった。だが巻き込まれた生徒の一人には、「逆算して考えたことがすごい」と言われ、感動されてしまった。

　ちなみに感動したほうの生徒が試みていたのは、〜その２〜で紹介した入試問題の例２を参考にして、まず 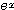を絡めた不等式を作ろうとしていた。残念ながらそれは不成功に終わってしまったのだが、筆者自身はそれを参考に、次のような証明をつくり、その生徒に紹介しておいた。

　(1)　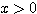 のとき 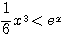を証明する。

　　ちなみに係数 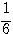も、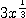 の 3 と全く同じ理由で、微分した際の余計な係数をなくすためである。

　　ただし 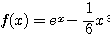とおいたとき、 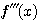まで必要であった。

　　　（さらに言えば、これは、大学初年度で学ぶ「テイラー展開」というものに関係する不等式である。）

　(2)　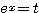 とおくことにより、(1)の不等式が次のように変形できることを利用する。

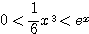
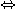
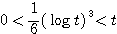
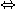
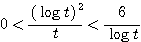
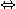
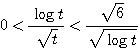
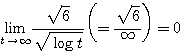　　　 であるからはさみうちの原理より 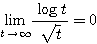すなわち

Others TOPへ

〜その５〜　調整　へ

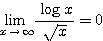
Copyright (C) 2004- imasen, All rights reserved.