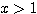 のとき
のとき 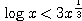 ・・・ (2) が成り立つか?
・・・ (2) が成り立つか?極限の強弱の証明 〜その5〜 調整
そこで調整として、
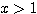 のとき
のとき 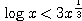 ・・・ (2) が成り立つか?
・・・ (2) が成り立つか?
を考えることにした。(1)との違いは、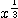 の係数に 3 をつけてみたことである。こうすれば次に示すように、
の係数に 3 をつけてみたことである。こうすれば次に示すように、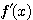 における
における 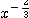 の係数
の係数 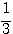 をなくすことができ、考えやすくなるかもしれないと思ったからだ。そして、結果的にこれは成功であった。
をなくすことができ、考えやすくなるかもしれないと思ったからだ。そして、結果的にこれは成功であった。
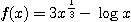
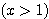 とおく。
とおく。
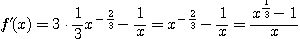 より、
より、
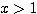 ではつねに
ではつねに 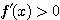 が成り立つから、
が成り立つから、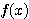 は単調増加。
は単調増加。
さらに、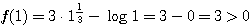
したがって、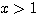 ではつねに
ではつねに 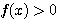 すなわち(2)が成り立つ。
すなわち(2)が成り立つ。
係数 3 があるおかげで、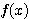 は単調増加になり、(2)が証明しやすくなったわけである。もちろんこのとき
は単調増加になり、(2)が証明しやすくなったわけである。もちろんこのとき 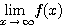 の計算も不要である。
の計算も不要である。
これでようやく不等式が作れた。
ひとたび不等式さえ作れれば、あとはそれを用いてはさみうちにするだけだ。
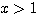 のとき
のとき 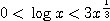 が成り立つ。辺々を
が成り立つ。辺々を 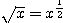 で割ることを考えると、
で割ることを考えると、
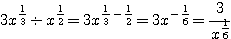 であることから
であることから
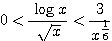
となる。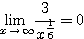 であるからはさみうちの原理より、
であるからはさみうちの原理より、
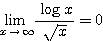
が成り立つことが示された。
Copyright (C) 2004- imasen, All rights reserved.