三角形の形状決定　～その２～

　問題：△ABC について等式

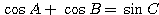
　が成り立つとき、この三角形の形状を決定せよ。

　・・・この問題に正弦定理・余弦定理を用いて、条件式を辺（長さ）の関係式に直して解くことを考えてみる。

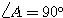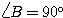　ややフライング気味だが、すでに答えはまたはの直角三角形と求められているから、

　　　　　，　　　，　　　，　　

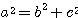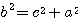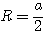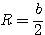
　などの結論が得られるはずだ。

　気持ちの上では、余弦定理よりもシンプルな正弦定理を用いたい。そこでまず条件式を次のように変形してみた。

　解答（その１）：

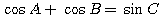
　の両辺を 2 乗して、

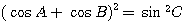
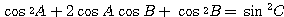
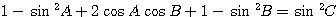
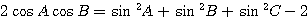
　この式の両辺をさらに 2 乗して、

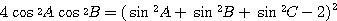
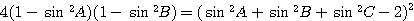
　これで（だいぶ大変そうな式だが）、条件が sin だけの式となった。

　ところが、ここに正弦定理の式を代入しても、うまく因数分解したり、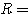の形にしたりすることが残念ながらできず、この方法はここで断念することとなった。

　そこで方針を変更して、今度は条件を cos だけの式に直し、余弦定理を用いることを考えた。