三角形の形状決定 〜その１〜
最近ではそんなに多く見られないが、1つの三角形で成り立つ関係式を三角比を用いて表し、その三角形の形状を求める問題がある。それを「三角形の形状決定問題」という。
例題：△ABC について等式
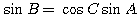
が成り立つとき、この三角形の形状を決定せよ。
考え方は、次の2つのうち、どちらかの方法をとることだ。
１． 正弦定理・余弦定理を用いて、条件を辺（長さ）の関係式で表す（数学１三角比の方法）。
２． 倍角・半角・積→和・和→積の公式を用いて、条件を角の関係式で表す（数学２三角関数の方法）。
大体の場合は１．でわりと簡単に解決することが多い。たとえば上に挙げた例題の解答は次のようになる。
解答：
正弦定理より、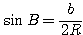
，
(
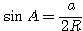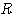は △ABC の外接円の半径)、余弦定理より、
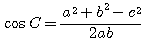であるから、これらを与えられた条件式に代入して、
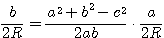
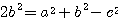
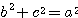
三平方の定理の逆より、△ABC は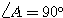 
の直角三角形。
ところが筆者が担当している授業のテキストで、次のような問題を２．を使って解いていた。ほかの参考書などでも同じ問題を同じ方法で解いている。
問題：△ABC について等式
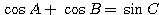
が成り立つとき、この三角形の形状を決定せよ。
条件式自体はシンプルである。これを模範解答どおり解くと、次のようになる。
解答：
左辺に和を積に直す公式（現行課程では数学３の範囲）を用いると、
(左辺)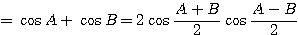
・・・(1)
となる。一方右辺に2倍角の公式を用いると、
(右辺) 
(∵ 
)
(∵ 
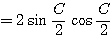
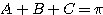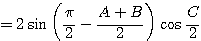
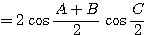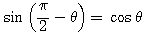) ・・・(2)
となる。(1)(2)を条件式に代入して、
(∵ 
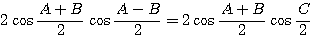
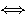
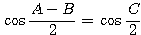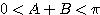より 
)
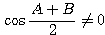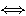
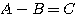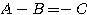
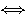
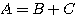または 
または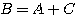 
よって、△ABC 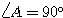は 
または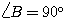 
の直角三角形。
ところが、同じ「三角形の形状決定問題」なのに、条件式によって解答を変えることは、筆者としてはいささか気に食わない。そこで、この問題も１．の方法で解けないかを試してみた。
Copyright (C) 2004- imasen, All rights reserved.