反転の問題　〜その２〜

　そこでまず、次の(★)を証明しておく。

　(★)　反転の条件を満たす点の組 (P, Q) および (P0, Q0) に対して、つねに

　　　　　△OP0P ∽　△OQQ0

　が成り立つ。

　（証明）　まず ∠P0OP=∠QOQ0　（共通）　・・・(1)　である。

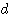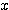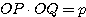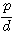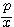　次に OP0=，OP= とすると、 により、OQ0=，OQ= である。

　このとき、

　　　OP0 : OQ 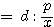 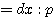　，　OP : OQ0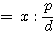

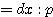
　であるから、OP0 : OQ = OP : OQ0　・・・(2)　である。

　(1)(2)から二辺比夾角相等により、△OP0P ∽　△OQQ0 が成り立つ　■

これを元に、反転の性質(2)〜(4)を図形的に証明してみることにしよう。

〜その３〜へ

〜その１〜へ

Others TOP へ

Copyright (C) 2004- imasen, All rights reserved.