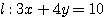 がある。
がある。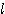 上に点 P をとり、半直線 OP 上に点 Q を、
上に点 P をとり、半直線 OP 上に点 Q を、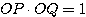 を満たすようにとる。P が
を満たすようにとる。P が 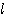 上を動くとき、点 Q の軌跡を求めよ。
上を動くとき、点 Q の軌跡を求めよ。反転の問題 〜その1〜
今回はまず、問題を見ていただこう。
-------------------------------------------------------------------------------------------
問題: O を原点とする座標平面上に直線 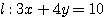 がある。
がある。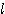 上に点 P をとり、半直線 OP 上に点 Q を、
上に点 P をとり、半直線 OP 上に点 Q を、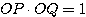 を満たすようにとる。P が
を満たすようにとる。P が 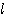 上を動くとき、点 Q の軌跡を求めよ。
上を動くとき、点 Q の軌跡を求めよ。
解答: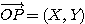 ,
,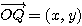 とおく。このとき条件
とおく。このとき条件 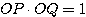 より、
より、
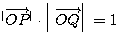 すなわち
すなわち 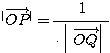 ・・・(1)
・・・(1)
が成り立つ。また、3 点 O,P,Q は同一半直線上にあることより、
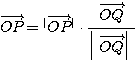 ・・・(2)
・・・(2)
が成り立つ。Q が原点に一致することはないので 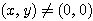 に注意して、(1)(2)より、
に注意して、(1)(2)より、
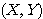
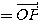
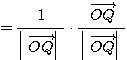
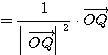
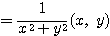
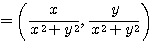 ・・・(3)
・・・(3)
ここで、点 P は直線 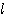 上を動くから、
上を動くから、
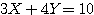 ・・・(4)
・・・(4)
を満たすので、(3)を(4)に代入して、
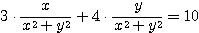
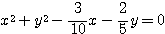
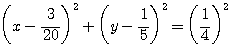
したがって Q の軌跡は、中心 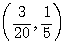 、半径
、半径 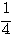 の円。ただし、
の円。ただし、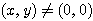 より、原点を除く。
より、原点を除く。
-------------------------------------------------------------------------------------------
これは、「反転の問題」という有名な問題だ。反転とは、点 P に対して、次のような条件(1)(2)を満たす点 Q をとるとき、点 P を点 Q に移す操作のことをいう。
反転の条件:
(1) 点 Q は半直線 OP 上にある
(2) 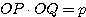 (長さの積が一定)
(長さの積が一定)
この反転について、次のが成り立つことが知られている。
反転の性質:
(1) O を通る直線は、O を通る直線に移る
(2) O を通らない直線は、O を通る円に移る
(3) O を通る円は、O を通らない直線に移る
(4) O を通らない円は、O を通らない円に移る
今回の問題は、(2)の一例であった。
このうち(1)は自明(直線 OP が直線 OP 自身に移る)だが、他のものはそうではない。もちろんその証明をするための一つの方法は、この問題のように座標平面上で計算することだ。だが今回は、それを図形的に証明してみることにした。
Copyright (C) 2004- imasen, All rights reserved.