Gauss-Greenの定理の証明
Step 1 符号つき面積
Oを原点とする座標平面上の△OABに対し、原点から見てO(0, 0), A(a, b), B(c, d)が「左回りのとき正、右回りのとき負」・・・(*)となるような△OABの面積を「符号つき面積」とよぶ。これをSとすると、
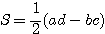
が成立する。
(証明)
OA, OBの長さをそれぞれ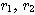 ,A, Bの偏角をそれぞれ
,A, Bの偏角をそれぞれ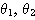 とする。ただし、
とする。ただし、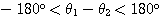 ,
,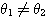 とする。
とする。
このとき、
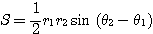
とすれば条件(*)を満たす。
ここで
A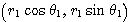 ,B
,B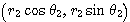
と表されることを利用して、

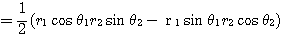
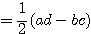 ■
■
Step 2 Gauss-Greenの定理
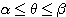 上の関数
上の関数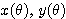 によって表される点P
によって表される点P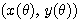 が座標平面上でA
が座標平面上でA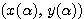 からB
からB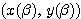 まで、原点から見て左回りに動くときに描く曲線を
まで、原点から見て左回りに動くときに描く曲線を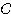 とする。曲線
とする。曲線 ,線分OA,および線分OBによって囲まれる図形の面積を
,線分OA,および線分OBによって囲まれる図形の面積を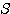 とするとき、
とするとき、
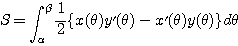
が成立する。Pが右回りに動くときも同じ式で面積を定める。このとき面積は負となる。
(証明)
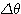 に対する増分をそれぞれ
に対する増分をそれぞれ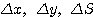 とすれば、Step1で示した符号つき面積の式より、
とすれば、Step1で示した符号つき面積の式より、
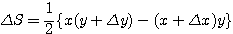
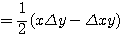
と近似できるから、
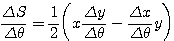
と表せる。
したがって、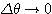 とすれば、
とすれば、
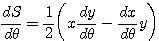
である。よって
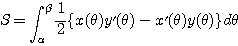
が成り立つ。■
パラメータ表示された閉曲線の内部の面積は、それが原点を内部に含んでいても、外部にあっても、符号つき面積の意味、およびこの定理によりすべて求められる。
原点を内部に含む場合、曲線 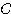 は原点から見てつねに左回りに進む。
は原点から見てつねに左回りに進む。
原点が外部にある場合、原点から曲線  に接線を 2 本引き、接点を図のように P1,P2
とおく。
に接線を 2 本引き、接点を図のように P1,P2
とおく。
P1 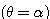 → P2
→ P2 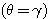 → P1
→ P1 
のように点 P が進むとし、さらに
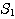 = (
= ( 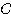 の P1 → P2
の部分と直線 OP1,OP2 により囲まれる部分の符号つき面積)
の P1 → P2
の部分と直線 OP1,OP2 により囲まれる部分の符号つき面積)
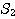 = (
= ( 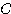 の P2 → P1
の部分と直線 OP1,OP2 により囲まれる部分の符号つき面積)
の P2 → P1
の部分と直線 OP1,OP2 により囲まれる部分の符号つき面積)
と定めれば、
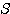 =
= 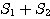
=
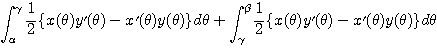
=
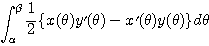
と表される。
Copyright (C) 2004- imasen, All rights reserved.