通り番外編 場合の数の使い分け（その６）
解答３．（ア）(1) 729 (2) 122 (3) 28 (4) 7 （イ）(1) 540 (2) 90 (3) 10 (4) 3
解説（ア）
(1) （重複順列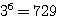） 通り
(2) （重複順列） この問題が一番難しくなってしまったので、解説は最後に・・・。
(3) （重複組合せ） 空箱があってもよいので ○○○○○○｜｜ を一緒に並べる。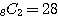
通り
(4) （地道に数える） (0, 0, 6) (0, 1, 5) (0, 2, 4) (0, 3, 3) (1, 1, 4) (1, 2, 3) (2, 2, 2) の7通り
（イ）
(1) （重複順列） （ア）(1)で数えた729通りから次の（ｉ）（ｉｉ）の場合を除く。
（ｉ） ちょうど2箱に分かれている場合
まず3箱中どの2箱を使うのかの選び方で
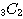通りあり、それに玉を分けるのは 
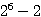通りずつある。
よって、この場合は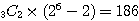 
通り
（ｉｉ） ちょうど1箱に分かれている場合 3通り
したがって、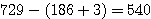
通り
(2) （重複順列） この問題も（ア）(2)とまとめて、解説は最後に・・・。
(3) （重複組合せ） 空箱があってはならないので、○∧○∧○∧○∧○∧○ ← ｜｜ 仕切りをスキマに入れて、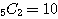
通り。
(4) （地道に数える） (1, 1, 4) (1, 2, 3) (2, 2, 2) の3通り
（ア）(2)・（イ）(2)の解説 （イ）(1)で「箱に区別がある」として数えたものから、箱の区別をなくせばよい。
（ｉ） ちょうど3箱に分かれている場合は、540通りある。
ここから箱の区別をなくせば、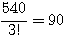
通り
（ｉｉ） ちょうど2箱に分かれている場合は、どの箱を選ぶかを考えずに数えれば
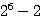通りある。
ここから箱の区別をなくせば、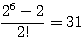 
通り
（ｉｉｉ） ちょうど1箱に分かれている場合は、3通りある。
ここから箱の区別をなくせば、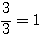
通り
したがって（ア）(2)は、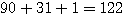
通り。（イ）(2)は、ちょうど3箱に分かれているものだけを数えて 90 通り。
******************************************************************
（ア）(2)は、次のように考えることもできる。
（ア）(4)で「玉に区別がつかない」として数えた7通りに、玉の区別をつければよい。いわゆる「組分け」の問題である。箱の区別はないから、（玉の個数が等しい箱の数）の階乗で割るのを忘れずに。
(0, 0, 6) → 
(0, 1, 5) →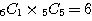 
(0, 2, 4) →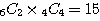 
(0, 3, 3) →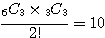 
(1, 1, 4) →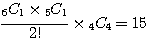 
(1, 2, 3) →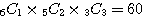 
(2, 2, 2) →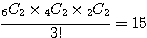 
したがって、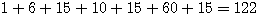
通り。
（イ）(2)も、(1, 1, 4) (1, 2, 3) (2, 2, 2) の3通りに組分けすればいいから、（ア）(2)の下3行を用いればよい。
したがって、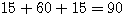
通り。
******************************************************************
筆者自身も、「場合の数」は慣れるのに時間がかかった。特に「順列」「組合せ」「重複順列」「重複組合せ」の4種類については、確かに一つ一つの問題の解き方は仕事上分かるけれど、今までの生徒に対して、その違いが100%明確に説明できたかどうかは、はっきり言って自信がなかった。
意欲のある2年生が、一年後の入試に備えて、早くもこの時期から「場合の数」を勉強し直していた。その生徒にとっても今回紹介した問題あたりがネックのようであった。今回の番外編はその生徒へ向けて書いたとも言える。
もちろん今年受験する人たちにとっても、今までもやもやしていた解き方が、少しでもはっきりすればいいなと思っている。そして、試験場でフルに力を出してほしいと思う。
Copyright (C) 2004- imasen, All rights reserved.