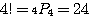イマセン第23回　何を同一視するか　～その１～

　今回は、場合の数の問題である。まずは例題から見てみよう。

例題：4 個の文字 a, b, c, d がある。

(1)　この 4 個を、一列に並べる方法は何通りあるか。

(2)　この 4 個を、円形に並べる方法は何通りあるか。

いわゆる「円順列」の問題である。セオリーを確認しておこう。

解答：

(1)　これは普通に「順列」の問題だから、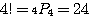通り。

(2)　これは「円順列」。円順列は、「回転して重なるものどうしを、すべて同じものとみなす」のがルールである。考え方は 2 つあった。

　（考え方１）　(1)の順列を円形につなげたとき、同じものをひとまとめにする方法。

　　(1)の 24 通りのうち、例えば次の 4 つの先頭と最後をつなげて円形にしたと考える。もともとの先頭を★で表す。

　　このとき、これらの 4 つは、順に右に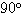ずつ回転すれば右隣のものに一致する。したがってこれらは、円順列としてはすべて同じものである。

　同様に他も 4 つずつ同じものだとみなせるので、円順列の方法は、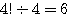通り。

　（考え方２）　考え方１の方法では、もともとの先頭であった★が aのもの、 bのもの、 cのもの、dのものが 1 つずつの計 4 つをまとめて同じものとすることができた。

　したがって円順列を数える場合、★にくるものが「aである」と決めてしまい、残り 3 個を並べる方法を考えればよい。この 3 個は普通の順列なので、その方法は、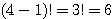通り。

　この結果は、次のようにまとめられる。

　異なる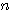個を円形に並べる方法（円順列）は、次の通り。

　　（考え方１：順列を円形にしたとき同じものをひとまとめにする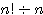）　・・・　　通り

　　（考え方２：1つのものを固定する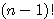）　・・・　　通り