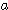イマセン第21回　動くものがたくさんあるときは　～その１～

　まずは、今回の問題を見ていただこう。

１．一辺の長さが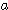である正四面体 O-ABC がある。辺 AB 上を点 P が、辺 OC 上を点 Q がそれぞれ動くとき、線分 PQ の長さの最小値を求めよ。

２．図のように、平面上に線分 AB と線分 MN がある。線分 AB 上を点 P が A から B まで動き、線分 MN 上を点 Q が M から N まで動くとき、線分 PQ の中点 R は、どのような図形をえがくか。

　ただし線分 AB と線分 MN は平行ではなく、交点ももたないとする。

　まずは、「PQ の長さが最小になるときがいつなのか」や「点 R のえがく図形がどうなるか」をイメージしてみてほしい。意外と難しいと思う。

　両方の問題に共通しているのは、「動くものが複数ある」こと。１．なら P，Q、２．なら P，Q，R だ。

　イメージしにくかった人は、動くものを一気に動かしていたからだろう。実はこういうとき、数学における考え方はだいたいいつも同じである。その考え方さえわかれば、どちらも中学生でも解ける問題だ。