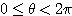のとき、不等式 
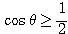を解け。イマセン第20回 基本に忠実に 〜その１〜
今日は、「教科書どおりのことは一通り分かるが、少しひねられると手も足も出ない」という人向けだ。単元は「数学２三角関数」、高校３年生以上の大学受験生は特に読んでもらいたい。
まずは例題から。
例題 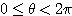のとき、不等式 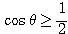を解け。
解答
１．まず与えられた範囲で、方程式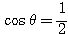 
を解くことを考える。
これは「単位円上の点の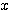 
座標が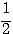 
に等しくなるような、角 
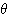の値」を求めることと同じである。
(1) 単位円の図に直線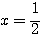 
を追加する。
(2) このとき円と直線とは交点を2つ持つ。
(3) 円の中心 O から (2) の2交点へ線分（動径）を引く。
(4) 下図斜線部の三角形は、辺の比が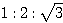 
の直角三角形である。
したがって、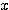
軸正の向き（始線）から動径までの角度は、それぞれ 
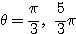である。
これが方程式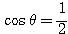 
の解である。
２．次に、不等式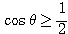 
を解くことを考える。
これは「単位円上の点の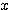 
座標が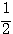 
以上となるような、角 
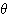の範囲」を求めることと同じである。
(5) 単位円上の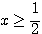 
の部分、すなわち、直線 
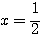よりも右側の部分を太く塗る。
(6) 太く塗った箇所に、0 と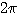 
が含まれることに注意して、求める範囲は 
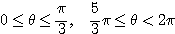となる。
これが不等式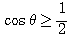 
の解である。
答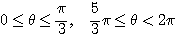 
どうだろうか。例題だけでずいぶんと長くなってしまったが、三角関数の不等式は苦手な人が多いので、じっくり解説してみた。
では次に、これを踏まえて問題に行こう。
Copyright (C) 2004- imasen, All rights reserved.