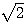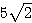
イマセン第19回　必要なものだけ残せ　～その４～

解答１．(3)　PQ = 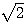，　QB =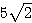

解説１．(3)

＜前半・PQ の長さ＞

　まず条件より BP = 6 であり、これと問題文にある BC = 8 から、PC = 2 が分かる。さらに問題文から AB = 6 であるから、直角三角形 ABP に注目すると AP = 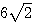も分かる。

　新しく分かった長さを図に書き込み、それらの長さが関係する直線 BC，線分 AP を太く塗ろう。

　そして、求めたい PQ, QB を太く塗る（図1-(3)-1）

　まず PQ の長さを求めるためには・・・、見えてきたかな？これも補足６－１．で挙げた方べきの定理の構図である（図1-(3)-2）。

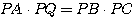　　　　　すなわち　　

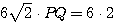
　したがって、PQ = 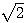と分かる。

＜後半・QB の長さ＞

　再び図1-(3)-1の太線部だけに注目してみる。線分 QB まで含めて考えると、こんどは図1-(3)-3のように、2つの相似な三角形が見えてくるだろうか。

　△PAC∽△PBQ であり、相似比は PA:PB = 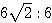= 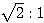である。問題文より AC=10 であるから、

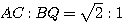　　　　　すなわち　

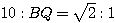
　したがって、QB = 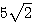であると分かる。