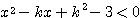イマセン第17回　条件を言い換える～４～

まず１で伝えたかったことは、問題文の不等号の向きにつられるな！ということだ。正しい答えは、

　(1)　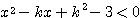　が解を持つ　→　

　(2)　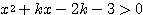　の解がすべての実数である　→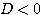　

だった。授業でこの話題が出てきたときには必ず注意するように言うのだが、どうしても(1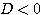)を，(2)をとしてしまう生徒が少なからずいる。ワンクッション、（ア）（イ）（ウ）のように考えてくれればよいのだが。

　それがきちんとできるようにするための特効薬はないが、まずこういった生徒は、その前段階である「２次不等式」の段階でつまずいている。それをしっかりマスターしてもらって上で改めてこの問題に臨むと、結構スムーズに理解してくれることが多い。

*************************************************************************************

　逆に２で伝えたかったことは、「かつ」「または」の言い換えさえきちんとできれば機械的に
　　「かつ」→掛け算・「または」→足し算
　にできる、ということだ。

　たとえば(3)において、

　　Aから赤球の確率は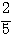，Bから赤球の確率は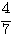，Aから白球の確率は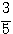，Bから白球の確率は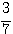

　であるから、

　「Aから赤球　かつ　Bから赤球」　または　「Aから白球　かつ　Bから白球」の確率は、いきなり、

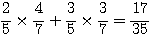
　と計算することができる。

　ただし、普通日本語で「AまたはB」と言った場合、「どちらか一方のみ」というニュアンスが暗に含まれる。

　たとえば今「俺は　カツ丼　または　カレーライス　を食う！」と宣言した人がいるとする（あまり日常会話っぽくはないけれど）。その人が両方とも食べてたら、不思議に思うのではないだろうか？

　ところが数学的に言えば、その人は正しい。なぜなら数学の「または」は「少なくとも一方を満たす」という意味なので、両方とも満たす場合もこれに含まれるからなのだ。

　そして場合分けをしたとき、もしも複数の場合を満たすものが存在すると、機械的に「または」を足し算とすることができない。

　たとえば(3)では、取り出された球の色が「両方とも赤」かつ「両方とも白」という場合はありえない（１つの球が片面ずつ赤と白に塗られているのなら別だが・・・）。

　したがって(3)では、大手を振って「または」を足し算にできる。　このように、複数の場合を満たすものがないように、「または」で場合分けすることを、「排反な事象に分ける」という。

　(3)の最後で「(i)(ii)は互いに排反より」と書いてあるのはそういう意味だ。

*************************************************************************************

　高校３年間で学ぶ数学の中で、どの学年の内容が一番難しいかと問われたら、筆者は間違いなく「高校１年生だ」と答える。それは次のような理由によるものだ。

　１．　機械的な計算だけではなく、「言い換えて」解く場面が多い（しかもそれは公式化できないこともある）。

　２．　かといって問題２(1)(2)のように、「知らなければ解けない」ものもけっこうある。

　これに比べれば２～３年生の難しさなんて、所詮「新しい記号のとっつきにくさ」「計算の面倒くささ」に尽きる。これは筆者に言わせると、「難しい」ではなく「ややこしい」である。

　だから逆に１年生の段階できっちり数学を理解できたならば、「数学的な考え方」の素地がしっかりとできているので、そこから先はそれほど苦ではないだろう。

　もしこれを読んでいる皆さんが高校１年生ならば、今学んでいる数学をとにかくがむしゃらに解いてマスターして欲しい。もっと学年が上の人で、自分の数学力にイマイチ自信がない場合、１年生の、特に「２次関数」だけでもいいから、やり直してみてはどうだろうか。