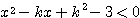 が解を持つような、定数
が解を持つような、定数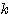 の値の範囲を求めよ。
の値の範囲を求めよ。イマセン第17回 条件を言い換える〜1〜
第13回では不等式を扱った。その補足で「パターン化せずに論理的に考えよう」と書いた。
「論理的に考える」というと難しく聞こえるが、むしろその逆である。難しかったり漠然としているように見える事柄でも、一つ一つ段階を踏んでクリアにしていけば、自ずと理解できるということである。
数学の場合、それは「条件を少しずつ、細かく言い換える」ということだ。
今回は「数学1・二次関数」「数学A・場合の数と確率」の教科書内容を単元を一通り学んでいることを前提とさせていただく。
問題1. (二次関数)
(1) 2次不等式 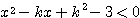 が解を持つような、定数
が解を持つような、定数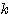 の値の範囲を求めよ。
の値の範囲を求めよ。
(2) 2次不等式 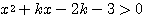 の解がすべての実数であるような、定数
の解がすべての実数であるような、定数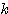 の値の範囲を求めよ。
の値の範囲を求めよ。
問題2. (場合の数と確率)
次の下線を引いた条件を「かつ」や「または」を使って言い換えよ。また、それぞれの場合の数や確率を求めよ。
-----------------------------------------------------------------------------------------
(例) 6種類の数字 0, 1, 2, 3, 4, 5 から異なる3個を選んで作る3桁の整数のうち、偶数であるものの個数。
→ 一の位が 0 または 2 または 4 である
場合の数を求めるためには、次のように場合分けする。
(i) 一の位が0の場合
残りの百・十の位に 1, 2, 3, 4, 5 のうち 2つを選んで入れる。
したがって、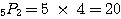 通り。
通り。
(ii) 一の位が2, 4の場合
一の位には、2か4の 2 通り。
残っている数字は 0, 1, 3, 5, □ (□は2, 4のどちらか)で0がまだ残っているから、
これを百の位に入れることはできないことに注意して、百の位には
4 通り。
十の位には、百の位で使った1つをさらに除いて 4 通り。
したがって、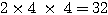 通り。
通り。
以上(i)(ii)より、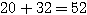 通り。
通り。
-----------------------------------------------------------------------------------------
(1) 6種類の数字 0, 1, 2, 3, 4, 5 から異なる3個を選んで作る3桁の整数のうち、5の倍数であるものの個数。
(2) 2桁の整数で、十の位と一の位の数の和が偶数となるものの個数。
(3) 赤球2個と白球3個が入った袋A、赤球4個と白球3個が入った袋Bがある。それぞれの袋から球を1個ずつ取り出すとき、取り出した2個の球が同色である確率。
Copyright (C) 2004- imasen, All rights reserved.